题目内容
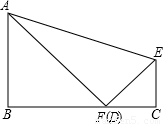
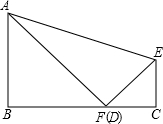如图，沿着折痕AE折叠矩形ABCD，使点D落在BC边上的点F处，已知∠AFB=38°，则∠AEF等于（ ）分析：利用折叠的性质可知．
解答：解：∵∠CED=∠AFB=38°
根据折叠前后角相等可知：∠AEF=（180-38）÷2=71°．
故选D．
根据折叠前后角相等可知：∠AEF=（180-38）÷2=71°．
故选D．
点评：本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．
练习册系列答案
相关题目
如图，把边长为AD=12cm，AB=8cm的矩形沿着AE为折痕对折使点D落在BC上点F处，求DE的长．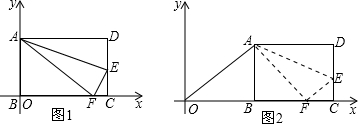
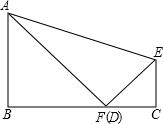如图，沿着折痕AE折叠矩形ABCD，使点D落在BC边上的点F处，已知∠AFB=38°，则∠AEF等于