题目内容
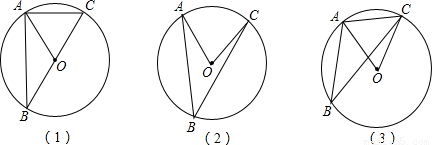
在探讨圆周角与圆心角的大小关系时,小亮首先考虑了一种特殊情况(圆心在圆周角的一边上)如图1所示:
∵∠AOC是△ABO的外角
∴∠AOC=∠ABO+∠BAO
又∵OA=OB
∴∠OAB=∠OBA
∴∠AOC=2∠ABO
即∠ABC= ∠AOC
∠AOC
如果∠ABC的两边都不经过圆心,如图2、3,那么结论会怎样?请你说明理由.
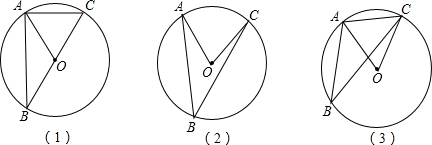
解:如果∠ABC的两边都不经过圆心,结论∠ABC= ∠AOC仍然成立.
∠AOC仍然成立.
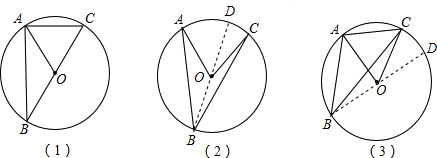
证明:∠ABC的两边都不经过圆心,对图2的情况,
连接BO并延长交圆O于点D,
由图1知:∠ABD= ∠AOD,∠CBD=
∠AOD,∠CBD= ∠COD
∠COD
∴∠ABD+∠CBD= ∠AOD+
∠AOD+ ∠COD
∠COD
∴∠ABC= ∠AOC
∠AOC
∠ABC的两边都不经过圆心,对图3的情况,连接BO并延长交圆O于点D
由图1知:∠ABD= ∠AOD,∠CBD=
∠AOD,∠CBD= ∠COD
∠COD
∴∠ABD-∠CBD= ∠AOD-
∠AOD- ∠COD
∠COD
∴∠ABC= ∠AOC.
∠AOC.
分析:连接BO并延长交圆O于点D,利用图1和结论求证.
点评:本题是圆周角定理的证明.在证明过程中要注意前后两个题目之间的联系,注意题目之间的转化.
 ∠AOC仍然成立.
∠AOC仍然成立.证明:∠ABC的两边都不经过圆心,对图2的情况,
连接BO并延长交圆O于点D,

由图1知:∠ABD=
 ∠AOD,∠CBD=
∠AOD,∠CBD= ∠COD
∠COD∴∠ABD+∠CBD=
 ∠AOD+
∠AOD+ ∠COD
∠COD∴∠ABC=
 ∠AOC
∠AOC∠ABC的两边都不经过圆心,对图3的情况,连接BO并延长交圆O于点D
由图1知:∠ABD=
 ∠AOD,∠CBD=
∠AOD,∠CBD= ∠COD
∠COD∴∠ABD-∠CBD=
 ∠AOD-
∠AOD- ∠COD
∠COD∴∠ABC=
 ∠AOC.
∠AOC.分析:连接BO并延长交圆O于点D,利用图1和结论求证.
点评:本题是圆周角定理的证明.在证明过程中要注意前后两个题目之间的联系,注意题目之间的转化.

练习册系列答案
相关题目
 ∠AOC
∠AOC
 ∠AOC
∠AOC
 ∠AOC
∠AOC