题目内容
 (2013•岱山县模拟)如图,Rt△ABC中,∠C=90°,以点B为圆心,适当长为半径画弧,与∠ABC的两边相交于点E,F,分别以点E和点F为圆心,大于
(2013•岱山县模拟)如图,Rt△ABC中,∠C=90°,以点B为圆心,适当长为半径画弧,与∠ABC的两边相交于点E,F,分别以点E和点F为圆心,大于| 1 |
| 2 |
分析:根据已知求出△BEM≌△BFM,推出∠CBD=∠ABC,根据AAS证△CBD≌△NBD,求出S△BDC=S△BDN=10,证△BDN≌△ADN,求出S△ADN=S△BDN=10,即可求出答案.
解答:解: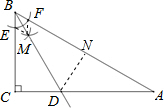
过D作DN⊥AB于N,连接EM、FM,
在△BEM和△BFM中
∵
,
∴△BEM≌△BFM,
∴∠CBD=∠ABD,
∵∠ABC=2∠A,∠C=90°,
∴3∠A=90°,
∴∠A=30°,∠ABC=60°,
∴∠ABD=∠CBD=30°=∠A,
在△CBD和△NBD中
∵
,
∴△CBD≌△NBD(AAS),
∴S△BDC=S△BDN=10,
∵在△BDN和△ADN中
,
∴△BDN≌△ADN(AAS),
∴S△ADN=S△BDN=10,
∴△ABC的面积是S△BCD+S△BDN+S△ADN=30,
故选B.

过D作DN⊥AB于N,连接EM、FM,
在△BEM和△BFM中
∵
|
∴△BEM≌△BFM,
∴∠CBD=∠ABD,
∵∠ABC=2∠A,∠C=90°,
∴3∠A=90°,
∴∠A=30°,∠ABC=60°,
∴∠ABD=∠CBD=30°=∠A,
在△CBD和△NBD中
∵
|
∴△CBD≌△NBD(AAS),
∴S△BDC=S△BDN=10,
∵在△BDN和△ADN中
|
∴△BDN≌△ADN(AAS),
∴S△ADN=S△BDN=10,
∴△ABC的面积是S△BCD+S△BDN+S△ADN=30,
故选B.
点评:本题考查了全等三角形的性质和判定,三角形的内角和定理,三角形的面积,含30度角的直角三角形等知识点,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013•岱山县模拟)如图,已知AB∥CD,若∠A=15°,∠E=25°,则∠C等于( )
(2013•岱山县模拟)如图,已知AB∥CD,若∠A=15°,∠E=25°,则∠C等于( )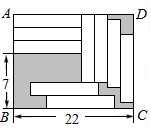 (2013•岱山县模拟)如图,矩形ABCD中放置9个形状、大小都相同的小矩形,相关数据图中所示,则图中阴影部分的面积为
(2013•岱山县模拟)如图,矩形ABCD中放置9个形状、大小都相同的小矩形,相关数据图中所示,则图中阴影部分的面积为