题目内容
【题目】如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则下面结论错误的是( ) 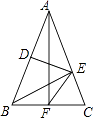
A.BF=EF
B.DE=EF
C.∠EFC=45°
D.∠BEF=∠CBE
【答案】B
【解析】解:∵AB=AC,AF⊥BC,
∴BF=FC,
∵BE⊥AC,
∴EF= ![]() BC=BF,A不合题意;
BC=BF,A不合题意;
∵DE= ![]() AB,EF=
AB,EF= ![]() BC,不能证明DE=EF,B符合题意;
BC,不能证明DE=EF,B符合题意;
∵DE垂直平分AB,
∴EA=EB,又BE⊥AC,
∴∠BAC=45°,
∴∠C=67.5°,又FE=FC,
∴∠EFC=45°,C不合题意;
∵FE=FB,
∴∠BEF=∠CBE;
故选:B.
【考点精析】认真审题,首先需要了解线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等),还要掌握等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角))的相关知识才是答题的关键.

练习册系列答案
相关题目