题目内容
如图，矩形ABCD中，由8个面积均为1的小正方形组成的L型模板如图放置，则矩形ABCD的周长为______．
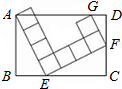
如图，连接AF，作GH⊥AE于点H，则有AE=EF=HG=4，FG=2，AH=2，
∵AG=
=2
，AF=
=4
，
∴AF2=AD2+DF2=（AG+GD）2+FD2=AG2+GD2+2AG•GD+FD2，GD2+FD2=FG2
∴AF2=AG2+2AG•GD+FG2∴32=20+2×2
×GD+4，
∴GD=
，FD=
，
∵∠BAE+∠AEB=90°=∠FEC+∠AEB，
∴∠BAE=∠FEC，
∵∠B=∠C=90°，AE=EF，
∴△ABE≌△ECF（AAS），
∴AB=CE，CF=BE，
∵BC=BE+CE=AD=AG+GD=2
+
，
∴AB+FC=2
+
，
∴矩形ABCD的周长=AB+BC+AD+CD=2BC+AB+CF+DF
=2
+
+2
+
+2
+
+
=8
．
故答案为，8
．
∵AG=
| AH2+HG2 |
| 5 |
| AE2+EF2 |
| 2 |
∴AF2=AD2+DF2=（AG+GD）2+FD2=AG2+GD2+2AG•GD+FD2，GD2+FD2=FG2
∴AF2=AG2+2AG•GD+FG2∴32=20+2×2
| 5 |
∴GD=
2
| ||
| 5 |
4
| ||
| 5 |
∵∠BAE+∠AEB=90°=∠FEC+∠AEB，
∴∠BAE=∠FEC，
∵∠B=∠C=90°，AE=EF，
∴△ABE≌△ECF（AAS），
∴AB=CE，CF=BE，
∵BC=BE+CE=AD=AG+GD=2
| 5 |
2
| ||
| 5 |
∴AB+FC=2
| 5 |
2
| ||
| 5 |
∴矩形ABCD的周长=AB+BC+AD+CD=2BC+AB+CF+DF
=2
| 5 |
2
| ||
| 5 |
| 5 |
2
| ||
| 5 |
| 5 |
2
| ||
| 5 |
4
| ||
| 5 |
| 5 |
故答案为，8
| 5 |
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
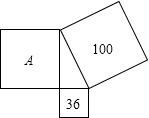
∠CFH都是锐角，已知EG=k，FH=l，四边形EFGH的面积为S，