题目内容
如图，△ABC中，∠C=90°，AC=4，BC=3．半径为1的圆的圆心P以1个单位/s的速度由点A沿AC方向在AC上移动，设移动时间为t（单位：s）．（1）当t为何值时，⊙P与AB相切；
（2）作PD⊥AC交AB于点D，如果⊙P和线段BC交于点E，证明：
当t=| 16 | 5 |
分析：（1）当⊙P在移动中与AB相切时，设切点为M，连接PM，根据△APM∽△ABC可求得t的值；
（2）由BC⊥AC，PD⊥AC，易得BC∥DP，再分别求得PD、BE的值，证明其相等，即可得出四边形PDBE为平行四边形的结论．
（2）由BC⊥AC，PD⊥AC，易得BC∥DP，再分别求得PD、BE的值，证明其相等，即可得出四边形PDBE为平行四边形的结论．
解答：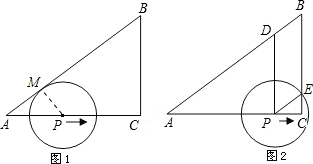
（1）解：当⊙P在移动中与AB相切时，
设切点为M，连接PM，则∠AMP=90°，
∴△APM∽△ABC，
∴
=
，
∵AP=t，AB=
=5，
∴
=
，
∴t=
．（4分）
（2）证明：∵BC⊥AC，PD⊥AC，
∴BC∥DP，
当t=
s时，AP=
，
∴PC=4-
=
，
∴EC=
=
=
∴BE=BC-EC=3-
=
，
∵△ADP∽△ABC，
∴
=
，
∴
=
，
∴PD=
，
∴PD=BE，
∴当t=
s时，四边形PDBE为平行四边形．
（1）解：当⊙P在移动中与AB相切时，设切点为M，连接PM，则∠AMP=90°，
∴△APM∽△ABC，
∴
| AP |
| AB |
| PM |
| BC |
∵AP=t，AB=
| AC2+BC2 |
∴
| t |
| 5 |
| 1 |
| 3 |
∴t=
| 5 |
| 3 |
（2）证明：∵BC⊥AC，PD⊥AC，
∴BC∥DP，
当t=
| 16 |
| 5 |
| 16 |
| 5 |
∴PC=4-
| 16 |
| 5 |
| 4 |
| 5 |
∴EC=
| PE2-PC2 |
12-(
|
| 3 |
| 5 |
∴BE=BC-EC=3-
| 3 |
| 5 |
| 12 |
| 5 |
∵△ADP∽△ABC，
∴
| PD |
| BC |
| AP |
| AC |
∴
| PD |
| 3 |
| ||
| 4 |
∴PD=
| 12 |
| 5 |
∴PD=BE，
∴当t=
| 16 |
| 5 |
点评：此题主要考查切线的性质、相似三角形的判定和性质以及平行四边形的判定．
练习册系列答案
相关题目
26、已知：如图，△ABC中，点D在AC的延长线上，CE是∠DCB的角平分线，且CE∥AB．
27、已知：如图，△ABC中，∠BAC=60°，D、E两点在直线BC上，连接AD、AE．
27、如图，△ABC中，AD⊥BC于D，DN⊥AC于N，DM⊥AB于M
14、如图，△ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，则∠C的大小是（ ）
已知，如图，△ABC中，点D在BC上，且∠1=∠C，∠2=2∠3，∠BAC=70°．