题目内容
(6分)
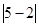 表示5与2差的绝对值,也可理解为5与2两数在数轴上所对应的两点之间的距离;
表示5与2差的绝对值,也可理解为5与2两数在数轴上所对应的两点之间的距离;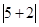 可以看做
可以看做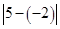 ,表示5与-2的差的绝对值,也可理解为5与-2两数在数轴上所对应的两点之间的距离.
,表示5与-2的差的绝对值,也可理解为5与-2两数在数轴上所对应的两点之间的距离.
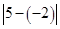 =___________.
=___________.
利用数轴,找出所有符合条件的整数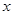 ,使
,使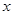 所表示的点到5和—2的距离之和为7
所表示的点到5和—2的距离之和为7
由以上探索猜想,对于任何有理数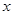 ,
,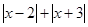 是否有最小值? 如果有,写出最
是否有最小值? 如果有,写出最
小值;如果没有,说明理由
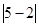 表示5与2差的绝对值,也可理解为5与2两数在数轴上所对应的两点之间的距离;
表示5与2差的绝对值,也可理解为5与2两数在数轴上所对应的两点之间的距离;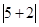 可以看做
可以看做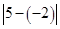 ,表示5与-2的差的绝对值,也可理解为5与-2两数在数轴上所对应的两点之间的距离.
,表示5与-2的差的绝对值,也可理解为5与-2两数在数轴上所对应的两点之间的距离.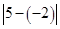 =___________.
=___________.利用数轴,找出所有符合条件的整数
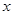 ,使
,使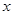 所表示的点到5和—2的距离之和为7
所表示的点到5和—2的距离之和为7由以上探索猜想,对于任何有理数
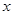 ,
,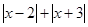 是否有最小值? 如果有,写出最
是否有最小值? 如果有,写出最 小值;如果没有,说明理由
(1)7 (2)-2,-1, 0, 1, 2,3, 4, 5 (3)有最小值,是5(每小题2分)
此题是信息类的题目,考查学生的阅读理解能力和自学能力,考查绝对值的含义;
(1)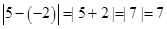 ;(2)因为5到-2的距离是7,所以在5和—2之间的任一个数包括5和-2所表示的点到5和—2的距离之和都为7,所以在5和—2的且到5和—2的距离之和为7的整数是-2,-1, 0, 1, 2,3, 4, 5 ;(3)
;(2)因为5到-2的距离是7,所以在5和—2之间的任一个数包括5和-2所表示的点到5和—2的距离之和都为7,所以在5和—2的且到5和—2的距离之和为7的整数是-2,-1, 0, 1, 2,3, 4, 5 ;(3)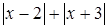 表示到-2和3的距离之和,要是最小只有在-2和3之间的数,所以最小距离是5;
表示到-2和3的距离之和,要是最小只有在-2和3之间的数,所以最小距离是5;
(1)
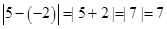 ;(2)因为5到-2的距离是7,所以在5和—2之间的任一个数包括5和-2所表示的点到5和—2的距离之和都为7,所以在5和—2的且到5和—2的距离之和为7的整数是-2,-1, 0, 1, 2,3, 4, 5 ;(3)
;(2)因为5到-2的距离是7,所以在5和—2之间的任一个数包括5和-2所表示的点到5和—2的距离之和都为7,所以在5和—2的且到5和—2的距离之和为7的整数是-2,-1, 0, 1, 2,3, 4, 5 ;(3)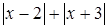 表示到-2和3的距离之和,要是最小只有在-2和3之间的数,所以最小距离是5;
表示到-2和3的距离之和,要是最小只有在-2和3之间的数,所以最小距离是5;
练习册系列答案
相关题目
 的相反数是( )
的相反数是( )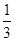

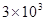 有一个有效数字
有一个有效数字

 +x
+x +x
+x +…+x
+…+x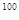 =_________
=_________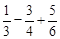 )+(-32)÷2
)+(-32)÷2 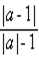 的值是( )
的值是( ) 的值是____.
的值是____.