题目内容
如图,小明将一块边长为2
的正方形纸片折叠成领带形状,其中∠D′CF=30°,B点落在CF边上的B′处,则AB′的长为

| 3 |
3
-
| 2 |
| 6 |
3
-
.| 2 |
| 6 |

分析:作AG⊥EB′于点G,把△AEB′分成两个直角三角形,由翻折的性质可知,∠ECB′=∠D′CF=30°,先在Rt△EB′C中,由锐角的三角函数的概念求得B′E,进而再求得AG,GB′,最后在Rt△AGB′中由勾股定理求得AB′的值.
解答: 解:作AG⊥EB′于点G,连接AB′,
解:作AG⊥EB′于点G,连接AB′,
由题意知,∠ECB′=∠D′CF=30°,∠EB′C=90°,B′C=BC=2
,
则∠AEB′=∠B′EC=60°,
B′E=B′Ccot60°=2,
解得:AE=2
-2,
∵AG⊥EB′,
∴AG=AEsin60°=3-
,
EG=AEcos60°=
-1,
∴B′G=B′E-EG=3-
,
在Rt△AGB′中,AB′=
=
=3
-
.
故本题答案为:3
-
.
 解:作AG⊥EB′于点G,连接AB′,
解:作AG⊥EB′于点G,连接AB′,由题意知,∠ECB′=∠D′CF=30°,∠EB′C=90°,B′C=BC=2
| 3 |
则∠AEB′=∠B′EC=60°,
B′E=B′Ccot60°=2,
解得:AE=2
| 3 |
∵AG⊥EB′,
∴AG=AEsin60°=3-
| 3 |
EG=AEcos60°=
| 3 |
∴B′G=B′E-EG=3-
| 3 |
在Rt△AGB′中,AB′=
| AG2+B′G2 |
(3
|
| 2 |
| 6 |
故本题答案为:3
| 2 |
| 6 |
点评:此题主要考查了翻折的性质,直角三角形的性质,三角函数的概念、勾股定理等知识,得出AG,B′G的长是解题关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
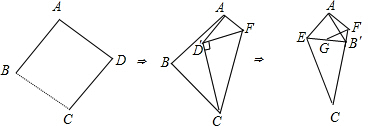
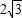 的正方形纸片折叠成领带形状,其中∠D′CF=30°,B点落在CF边上的B′处,则AB′的长为 .
的正方形纸片折叠成领带形状,其中∠D′CF=30°,B点落在CF边上的B′处,则AB′的长为 .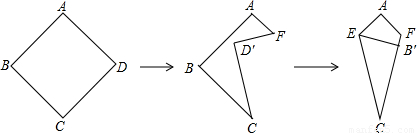
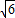 的正方形纸片折叠成领带形状,其中∠D′CF=30°,B点落在CF边上的B′处,则AB′的长为 .
的正方形纸片折叠成领带形状,其中∠D′CF=30°,B点落在CF边上的B′处,则AB′的长为 . 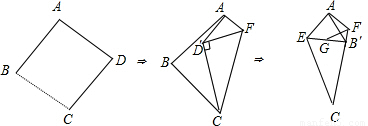
 的正方形纸片折叠成领带形状,其中∠D′CF=30°,B点落在CF边上的B′处,则AB′的长为 .
的正方形纸片折叠成领带形状,其中∠D′CF=30°,B点落在CF边上的B′处,则AB′的长为 . 