题目内容

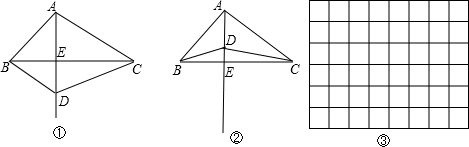
25、如图，过四边形ABCD的四个顶点分别作对角线AC、BD的平行线，所围成的四边形EFGH显然是平行四边形．

（1）当四边形ABCD分别是菱形、矩形、等腰梯形时，相应的平行四边形EFGH一定是“菱形、矩形、正方形”中的哪一种？请将你的结论填入下表：
（2）反之，当用上述方法所围成的平行四边形EFGH分别是矩形、菱形时，相应的原四边形ABCD必须满足怎样的条件？
分析：（1）原四边形是菱形时，菱形的对角线互相垂直，因此平行四边形应该是个矩形（平行四边形相邻的两边都垂直），
原四边形是矩形或等腰梯形时，它的对角线相等，那么平行四边形应该是个菱形（平行四边形相邻的两边都相等）；
（2）根据（1）我们可看出要想使得出的平行四边形是矩形，那么原四边形的对角线就必须垂直，因为只有这样平行四边形的相邻两边才垂直．同理平行四边形是菱形时，原四边形的对角线就必须相等．
解答：解：（1）四边形ABCD是菱形时，平行四边形EFGH是矩形，
四边形ABCD是矩形时，平行四边形EFGH是菱形，
四边形ABCD是等腰梯形时，平行四边形EFGH是菱形；

（2）当平行四边形是矩形时，原四边形ABCD必须满足的条件是对角线互相垂直，
当平行四边形是菱形时，原四边形ABCD必须满足的条件是对角线相等．
点评：本题主要考查了矩形的性质和判定，菱形的性质和判定，等腰梯形的判定等知识点．
练习册系列答案
相关题目
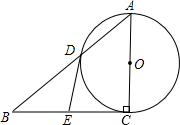如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线精英家教网，交BC于点E．
（1）求证：点E是边BC的中点；
（2）若EC=3，BD=2
6
，求⊙O的直径AC的长度；
（3）若以点O，D，E，C为顶点的四边形是正方形，试判断△ABC的形状，并说明理由．
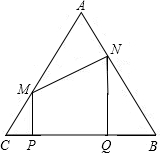如图，等边△ABC的边长为2，动点P，Q在线段BC上移动（都不与B，C重合），点P在Q的左精英家教网边，PQ=1，过点P作PM⊥CB，交AC于M，过点Q作QN⊥CB，交AB于N，连接MN．记CP的长为t．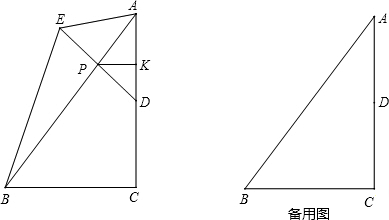
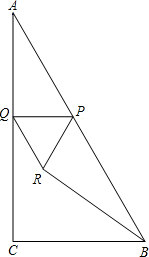（1）当t为何值时，四边形MPQN是矩形？
（2）设四边形MPQN的面积为S，请说明当P，Q移动时，S是否为定值？若是，求出这个定值；若不是，请求出S关于t的函数关系式；
（3）当t取何值时，以点C，P，M为顶点的三角形与以A，M，N为顶点的三角形相似．判断此时△MNP的形状，并请说出理由．
（2012•温州三模）如图，在Rt△ABC中，∠ACB=Rt∠，BC=3，AC=4，D是AC的中点，P是AB上一动点，连接DP并延长至点E，使EP=DP，过P作PK⊥AC，K为垂足．设AP=m（0≤m≤5）．
（1）用含m的代数式表示DK的长；
（2）当AE∥BC时，求m的值；
（3）四边形AEBC的面积S会随m的变化而变化吗？若不变，求出S的值；若变化，求出S与m的函数关系式；
（4）作点E关于直线AB的对称点E'，当△DE'K是等腰三角形时，求m的值．（直接写出答案即可）
（2012•平顶山一模）如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=10，P是AB边上的一个动点（异于A、B两点），过点P作PQ⊥AC于Q，以PQ为边向下作等边三角形PQR．设AP=x，△PQR与△ABC重叠部分的面积为y，连接RB．
（1）当x=2时，求y的值；
（2）当x取何值时，四边形AQRB是等腰梯形；当x取何值时，四边形PQRB是平行四边形．
如图，过△ABC的顶点A作AE⊥BC，垂足为E．点D是射线AE上一动点（点D不与顶点A重合），连结DB、DC．已知BC=m，AD=n．

（1）若动点D在BC的下方时（如图①），AE=3，DE=2，BC=6，求S四边形ABDC；
（2）若动点D在BC的下方时（如图①），求S四边形ABDC的值（结果用含m、n的代数式表示）；
（3）若动点D在BC的上方时（如图②），（1）中结论是否仍成立？说明理由；
（4）请你按以下要求在8×6的方格中（如图③，每一个小正方形的边长为1），设计一个轴对称图形．设计要求如下：对角线互相垂直且面积为6的格点四边形（4个顶点都在格点上）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网