题目内容
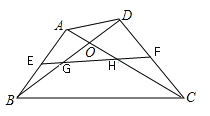
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,E、F分别相交是AB、CD的中点,EF分别交BD、AC于点G、H。求证:OG=OH。
【答案】证明见解析.
【解析】试题分析::取BC边的中点M,连接EM,FM,则根据三角形的中位线定理,即可证得△EMF是等腰三角形,根据等边对等角,即可证得∠MEF=∠MFE,然后根据平行线的性质证得∠OGH=∠OHG,根据等角对等边即可证得.
试题解析:∵M、F分别是BC、CD的中点,
∴MF∥BD,MF=![]() BD,
BD,
同理:ME∥AC,ME=![]() AC,
AC,
∵AC=BD
∴ME=MF
∴∠MEF=∠MFE,
∵MF∥BD,
∴∠MFE=∠OGH,
同理,∠MEF=∠OHG,
∴∠OGH=∠OHG
∴OG=OH.
考点: 三角形中位线定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】甲、乙、并三位同学参加数学综合素质测试![]() 各项成绩如下
各项成绩如下![]() 单位:分
单位:分![]()
同学 成绩 | 数与代数 | 图形与几何 | 统计与概率 | 综合与实践 |
甲 | 90 | 93 | 89 | 90 |
乙 | 94 | 92 | 94 | 86 |
丙 | 92 | 91 | 90 | 88 |
![]() 甲、乙、丙三位同学成绩的中位数分别为______;
甲、乙、丙三位同学成绩的中位数分别为______;
![]() 如果数与代数、图形与几何、统计与概率、综合与实践的成绩按3:3:2:2计算,分别计算甲、乙、丙三位同学的数学综合素质测试成绩,从成绩看,应推荐谁参加更高级别的比赛?
如果数与代数、图形与几何、统计与概率、综合与实践的成绩按3:3:2:2计算,分别计算甲、乙、丙三位同学的数学综合素质测试成绩,从成绩看,应推荐谁参加更高级别的比赛?