题目内容
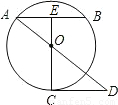
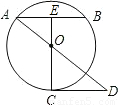
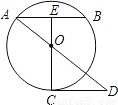
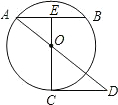 如图,已知AB为圆O的弦(非直径),E为AB的中点,EO的延长线交圆于点C,CD∥AB,且交AO的延长线于点D.EO:OC=1:2,CD=4,求圆O的半径.
如图,已知AB为圆O的弦(非直径),E为AB的中点,EO的延长线交圆于点C,CD∥AB,且交AO的延长线于点D.EO:OC=1:2,CD=4,求圆O的半径.
分析:根据E为AB的中点,则OE⊥AB,根据CD∥AB,可以得到△AEO∽△DCO,根据相似三角形的对应边的比相等,可以求出AE,在Rt△AOE中,根据勾股定理,就得到半径.
解答:解:∵E是AB的中点,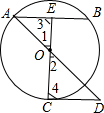
∴OE⊥AB,即∠3=90°,(1分)
∵AB∥CD,∴∠4=90°,(2分)
∵∠1=∠2,(3分)
∴△AOE∽△DOC,(4分)
∴AE:DC=OE:OC=1:2,(5分)
∴AE=
CD=2,(6分)
又∵OA=OC=2OE,(7分)
而AE2+OE2=OA2,
∴OE2+4=(2OE)2,
∴OE=
,(8分)
∴圆O的半径OA=2OE=
×2=
.(9分)
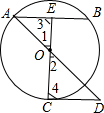
∴OE⊥AB,即∠3=90°,(1分)
∵AB∥CD,∴∠4=90°,(2分)
∵∠1=∠2,(3分)
∴△AOE∽△DOC,(4分)
∴AE:DC=OE:OC=1:2,(5分)
∴AE=
| 1 |
| 2 |
又∵OA=OC=2OE,(7分)
而AE2+OE2=OA2,
∴OE2+4=(2OE)2,
∴OE=
| 2 |
| 3 |
| 3 |
∴圆O的半径OA=2OE=
| 2 |
| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
点评:本题主要考查了垂径定理,利用勾股定理把求半径的问题转化为解方程的问题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
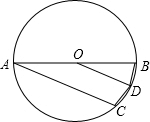 (2012•河东区二模)如图,已知AB为圆O直径,D是弧BC中点,若AC=8,AB=10,则BD=
(2012•河东区二模)如图,已知AB为圆O直径,D是弧BC中点,若AC=8,AB=10,则BD=