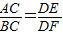题目内容
根据下列条件,能判断以a、b、c为边的三角形是直角三角形的是( )
A、a=
| ||||||
| B、a=32、b=42、c=52 | ||||||
C、a=
| ||||||
| D、a=3×8、b=4×8、c=5×8 |
分析:根据勾股定理的逆定理对四个选项进行逐一判断即可.
解答:解:A、∵a=
,b=
,c=
,c2+b2=(
)2+(
)2=
,a2=(
)2=
,c2+b2≠a2,∴此三角形不是直角三角形;
B、∵a=32、b=42、c=52,∴a2+b2=32+162=265≠c2=625,∴此三角形不是直角三角形;
C、∵a=
,b=
,c=
,a2+b2=(
)2+(
)2=7≠c2=(
)2=5,∴此三角形不是直角三角形;
D、∵a=3×8=24、b=4×8=32、c=5×8=40,
∴a2+b2=(24)2+(32)2=1600,c2=(40)2=1600,a2+b2=c2,∴此三角形是直角三角形;
故选D.
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 4 |
| 41 |
| 400 |
| 1 |
| 3 |
| 1 |
| 9 |
B、∵a=32、b=42、c=52,∴a2+b2=32+162=265≠c2=625,∴此三角形不是直角三角形;
C、∵a=
| 3 |
| 4 |
| 5 |
| 3 |
| 4 |
| 5 |
D、∵a=3×8=24、b=4×8=32、c=5×8=40,
∴a2+b2=(24)2+(32)2=1600,c2=(40)2=1600,a2+b2=c2,∴此三角形是直角三角形;
故选D.
点评:本题考查勾股定理的逆定理的应用.注:若有一组数是勾股数,同时扩大相同的倍数仍属勾股数,如:3,4,5是勾股数,则a=3×8、b=4×8、c=5×8还是勾股数.

练习册系列答案
相关题目
根据下列条件,能判断△ABC∽△DEF的是( )
| A、∠A=52°,∠B=58°;∠E=58°,∠F=80° | ||||
B、∠C=102°,∠E=102°;
| ||||
| C、AB=1,AC=1.5,BC=2;EF=8,DE=10,FD=16 | ||||
| D、∠C=∠F=Rt∠,AC=5,BC=13;DF=10,EF=26 |