题目内容
若圆周角α所对弦长为sinα，则此圆的半径r为分析：如图，过O作OC⊥AB于C，则∠D=∠AOC=α，根据三角函数的定义可以得到AC=
，
∴sin∠AOC=sinα=
=
．利用这个等式即可求出半径．
| sinα |
| 2 |
∴sin∠AOC=sinα=
| AC |
| AO |
| ||
| r |
解答：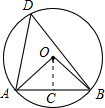
解：如图，过O作OC⊥AB于C，
由题意知∠D=∠AOC=α．
而AC=
，
∴sin∠AOC=sinα=
=
，
∴r=
．
解：如图，过O作OC⊥AB于C，由题意知∠D=∠AOC=α．
而AC=
| sinα |
| 2 |
∴sin∠AOC=sinα=
| AC |
| AO |
| ||
| r |
∴r=
| 1 |
| 2 |
点评：本题圆周角定理、垂径定理和锐角三角函数的概念．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
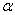所对弦长为sin