Question

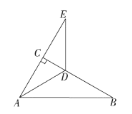
【题目】如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AD平分∠CAB.

（1）求∠CAD的度数；

（2）延长AC至E，使CE=AC，试说明DA=DE.

Answer 1

【答案】（1）30（2）见解析

【解析】

（1）利用“直角三角形的两个锐角互余”的性质和角平分的性质进行解答；

（2）通过证△ACD≌△ECD来推知DA＝DE．

（1）∵在Rt△ABC中，∠ACB＝90，∠B＝30，

∴∠B＝30，

∴∠CAB＝60．

又∵AD平分∠CAB，

∴∠CAD＝∠CAB＝30，即∠CAD＝30；

（2）证明：∵∠ACD＋∠ECD＝180，且∠ACD＝90，

∴∠ECD＝90，

∴∠ACD＝∠ECD．

在△ACD与△ECD中，

，

∴△ACD≌△ECD（SAS），

∴DA＝DE．