题目内容
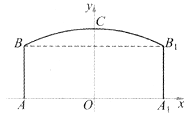
如图,隧道的截面由抛物线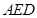 和矩形
和矩形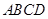 构成,矩形的长
构成,矩形的长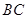 为
为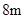 ,宽
,宽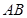 为
为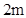 ,以
,以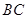 所在的直线为
所在的直线为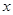 轴,线段
轴,线段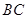 的中垂线为
的中垂线为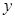 轴,建立平面直角坐标系,
轴,建立平面直角坐标系,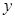 轴是抛物线的对称轴,顶点
轴是抛物线的对称轴,顶点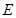 到坐标原点
到坐标原点 的距离为
的距离为 .
.
(1)求抛物线的解析式;
 (2)一辆货运卡车高
(2)一辆货运卡车高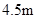 ,宽2.4m,它能通过该隧道吗?
,宽2.4m,它能通过该隧道吗?
(3)如果该隧道内设双行道,为了安全起见,在隧道正中间设
有0.4m的隔离带,则该辆货运卡车还能通过隧道吗?
(1)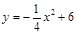 (-4≤x≤4)
(-4≤x≤4)
(2)当x=1.2时,y=5.64>4.5, 能通过。
(3)当x=0.2+2.4=2.6时,y=4.31<4.5,不能通过。
【解析】分析:由题意,不难确定抛物线顶点坐标为E(0,6),且过点A(﹣4,2),D(4,2),则可求其解析式;汽车通过隧道而不能碰到隧道顶部,实际上可借助于抛物线。通过确定抛物线上点F的横坐标,从而获得答案。汽车可以从隧道的正中间走,则F点横坐标为(1.2,纵坐标代入抛物线解析式中求得,再与4.5比较即可。
解:
(1)设抛物线解析式为y=ax2+bx+c
由题意得:
16a+4b+c=2 a=-1/4
16a-4b+c=2 解得: b=0
c=6
所以,y=﹣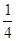 x2+6
x2+6
(2)货运卡车从隧道正中间走,如图,则点F的横坐标为1.2,因此,当x=1.2时,y= ﹣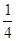 ×1.22+6=﹣0.38+6=5.62>4.5
×1.22+6=﹣0.38+6=5.62>4.5
因此,这辆货运卡车能通过该隧道。
(3)隧道正中间如果设有0.4m的隔离带,那么该货运卡车紧贴着隔离带靠右边形式时则点P的横坐标为0.2+2.4=2.56,所以,当x=1.2时,
y= ﹣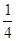 ×1.22+6=﹣1.69+6=4.31<4.5
×1.22+6=﹣1.69+6=4.31<4.5
所以,这辆货运卡车不能通过该隧道。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 的距离为8m.
的距离为8m.