题目内容
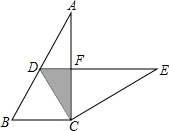 (2013•呼伦贝尔)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,将△ABC绕点C顺时针方向旋转60°后得到△EDC,此时点D在斜边AB上,斜边DE交AC于点F.则图中阴影部分的面积为( )
(2013•呼伦贝尔)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,将△ABC绕点C顺时针方向旋转60°后得到△EDC,此时点D在斜边AB上,斜边DE交AC于点F.则图中阴影部分的面积为( )分析:根据直角三角形两锐角互余求出∠B=60°,根据旋转变换只改变图形的位置不改变图形的形状与大小可得CD=BC,再求出∠ACD=30°,∠CFD=90°,解直角三角形求出DF、CF,然后利用三角形的面积公式列式计算即可得解.
解答:解:∵∠ACB=90°,∠A=30°,
∴∠B=90°-30°=60°,
∵△ABC绕点C顺时针方向旋转60°后得到△EDC,点D在斜边AB上,
∴∠BCD=60°,CD=BC=2,
∴∠ACD=∠ACB-∠BCD=90°-60°=30°,
∠CFD=180°-30°-60°=90°,
在Rt△CDF中,DF=
CD=
×2=1,
CF=
=
=
,
∴阴影部分的面积=
DF•CF=
×1×
=
.
故选C.
∴∠B=90°-30°=60°,
∵△ABC绕点C顺时针方向旋转60°后得到△EDC,点D在斜边AB上,
∴∠BCD=60°,CD=BC=2,
∴∠ACD=∠ACB-∠BCD=90°-60°=30°,
∠CFD=180°-30°-60°=90°,
在Rt△CDF中,DF=
| 1 |
| 2 |
| 1 |
| 2 |
CF=
| CD2-DF2 |
| 22-12 |
| 3 |
∴阴影部分的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
故选C.
点评:本题考查了旋转的性质,直角三角形两锐角互余,熟记性质并求出△CDF是有一个角是30°的直角三角形是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目