题目内容
若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角为
- A.30
- B.45
- C.60
- D.90
A
分析:将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的长度与矩形相等的一条边上的高为矩形的一半,即AB=2AE.
解答: 解:将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,
解:将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,
平行四边形ABCD是原矩形变化而成,
∴FG=BC,FH=2AE.
又∵HF=AB,
∴AB=2AE,
在Rt△ABE中,AB=2AE,
∠B=30°.
故选A.
点评:本题考查了矩形各内角为90°的性质,平行四边形面积的计算方法,特殊角的三角函数,本题中利用特殊角的正弦函数是解题的关键.
分析:将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的长度与矩形相等的一条边上的高为矩形的一半,即AB=2AE.
解答:
 解:将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,
解:将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,平行四边形ABCD是原矩形变化而成,
∴FG=BC,FH=2AE.
又∵HF=AB,
∴AB=2AE,
在Rt△ABE中,AB=2AE,
∠B=30°.
故选A.
点评:本题考查了矩形各内角为90°的性质,平行四边形面积的计算方法,特殊角的三角函数,本题中利用特殊角的正弦函数是解题的关键.

练习册系列答案
相关题目
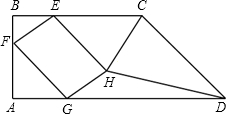 G分别在BC、AB、AD上,且BE=3,BF=2,以EF、FG为邻边作?EFGH,设AG=x.
G分别在BC、AB、AD上,且BE=3,BF=2,以EF、FG为邻边作?EFGH,设AG=x.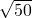 •
•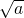 的值是一个整数,则正整数a的最小值是
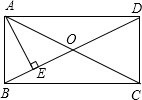
的值是一个整数,则正整数a的最小值是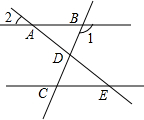 如图,已知AB∥CE,AE与BC交于点D,∠1=120°,∠2=30°,则下列说法不正确的
如图,已知AB∥CE,AE与BC交于点D,∠1=120°,∠2=30°,则下列说法不正确的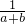
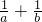
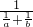
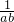
 如图,在矩形ABCD中,对角线AC,BD交于点O,AE⊥BD于点E,∠AOB=45°,则∠BAE的大小为
如图,在矩形ABCD中,对角线AC,BD交于点O,AE⊥BD于点E,∠AOB=45°,则∠BAE的大小为 如图,将纸片△ABC沿着DE折叠压平,且∠1+∠2=72°,则∠A=
如图,将纸片△ABC沿着DE折叠压平,且∠1+∠2=72°,则∠A=