题目内容
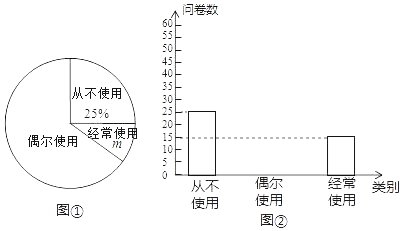
【题目】某校申报“跳绳特色运动”学校一年后,抽样调查了部分学生的“1分钟跳绳”成绩,并制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图.
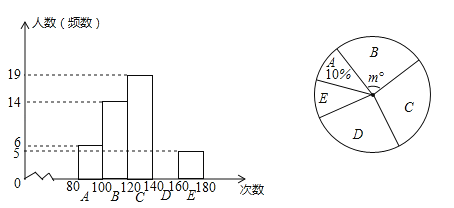
(1)补全频数分布直方图,扇形图中m= ;
(2)若把每组中各个数据用这组数据的中间值代替(如A组80≤x<100的中间值是(![]() =90次),则这次调查的样本平均数是多少;
=90次),则这次调查的样本平均数是多少;
(3)如果“1分钟跳绳”成绩大于或等于120次为优秀,那么该校2100名学生中“1分钟跳绳”成绩为优秀的大约有多少人.
【答案】(1)84;(2)130;(3)1400.
【解析】
(1)首先由第二小组有10人,占20%,可求得总人数,再由各小组频数之和等于数据总数求得第四小组的人数,作出统计图,先求出第一小组所占百分比,再乘以360°即可求出对应扇形圆心角的度数;
(2)由加权平均数的计算公式求出平均数即可;
(3)求出样本中成绩优秀的人数所占的百分比,用样本估计总体即可.
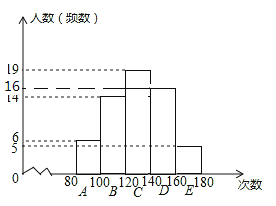
解:(1)由直方图和扇形图可知,A组人数是6人,占10%,则总人数:6÷10%=60,m=![]() ×360°=84°,D组人数为:60﹣6﹣14﹣19﹣5=16,
×360°=84°,D组人数为:60﹣6﹣14﹣19﹣5=16,
故答案为:84;
补全图形如图:
 ;
;
(2)平均数是:![]() =130;
=130;
(3)绩为优秀的大约有:2100×![]() =1400人;
=1400人;

练习册系列答案
相关题目