Question

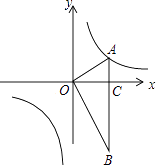
【题目】如图，在矩形ABCD中，AB=2，BC=4，点M、N分别在边AD和BC上，沿MN折叠四边形ABCD，使点A、B分别落在A1、B1处，得四边形A1B1NM，其中点B1在DC上，过点M作ME⊥BC于点E，连接BB1 ， 给出下列结论：①∠MNB1=∠ABB1；②△MEN∽△BCB1；③ 的值为定值；④当B1C= DC时，AM= ，其中正确结论的序号是 ． （把所有正确结论的序号都在填在横线上）

Answer 1

【答案】①②③
【解析】解：由折叠可知∠MNB1=∠BNM，MN⊥BB1，

∴∠BNM+∠B1BN=90°，

∵∠ABB1+∠B1BN=90°，

∴∠BNM=∠ABB1，

∴∠MNB1=∠ABB1，故①正确；

∵ME⊥BC，

∴∠MNE+∠NME=90°，

由由折叠的性质可得MN⊥BB1，

∴∠MNE+∠B1BN=90°，

∴∠NME=∠BB1N，

∴△MEN∽△BCB1，

故②正确；

由②可知 = ，

∵ME=AB=2，BC=4，

∴ = = ，为定值，故③正确；

∵△MEN∽△BCB1，

∴ = = ，

∴NE= B1C，

若B1C= DC，

则NE= DC= ×2= ，

设BN=x，则NC=4﹣x，B1N=x，

在Rt△B1NC中，由勾股定理可得x2=（4﹣x）2+12，

解得x= ，

∴AM=BE=BN﹣NE= ﹣ = ，故④不正确．

所以答案是：①②③．

【考点精析】根据题目的已知条件，利用矩形的性质和翻折变换（折叠问题）的相关知识可以得到问题的答案，需要掌握矩形的四个角都是直角，矩形的对角线相等；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．