题目内容
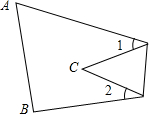 如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠2=20°,则∠1的度数为
如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠2=20°,则∠1的度数为
- A.30°
- B.45°
- C.60°
- D.无法确定
C
分析:由∠A、∠B的度数,可求∠C的大小,进而在△CDE中,得出∠CDE与∠CED的和,再在四边形ABED中,即可求解∠1的大小.
解答: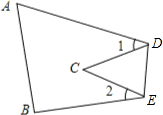 解:如图,∵∠A=65°,∠B=75°,则∠C=40°,
解:如图,∵∠A=65°,∠B=75°,则∠C=40°,
在△CDE中,则∠CDE+∠CED=140°,
在四边形ABED中,∠A+∠B+∠ADE+∠BED=360°,
即∠A+∠B+∠CDE+∠1+∠2+∠CED=360°,
65°+75°+140°+20°+∠1=360°,
∠1=60°.
故选C.
点评:本题主要是考查了三角形、四边形内角和的运用,能够利用其内角和求解一些简单的计算问题.
分析:由∠A、∠B的度数,可求∠C的大小,进而在△CDE中,得出∠CDE与∠CED的和,再在四边形ABED中,即可求解∠1的大小.
解答:
 解:如图,∵∠A=65°,∠B=75°,则∠C=40°,
解:如图,∵∠A=65°,∠B=75°,则∠C=40°,在△CDE中,则∠CDE+∠CED=140°,
在四边形ABED中,∠A+∠B+∠ADE+∠BED=360°,
即∠A+∠B+∠CDE+∠1+∠2+∠CED=360°,
65°+75°+140°+20°+∠1=360°,
∠1=60°.
故选C.
点评:本题主要是考查了三角形、四边形内角和的运用,能够利用其内角和求解一些简单的计算问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
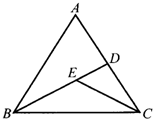 24、如图,∠A=65°,∠ABD=∠DCE=30°,求∠BEC的度数.
24、如图,∠A=65°,∠ABD=∠DCE=30°,求∠BEC的度数.
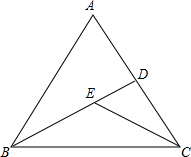 如图:∠A=65°,∠ABD=∠DCE=30°,且CE平分∠ACB,求∠BEC的度数.
如图:∠A=65°,∠ABD=∠DCE=30°,且CE平分∠ACB,求∠BEC的度数.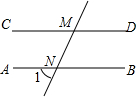 如图,∠1=65°,∠DMN=115°,求证:CD∥AB.
如图,∠1=65°,∠DMN=115°,求证:CD∥AB.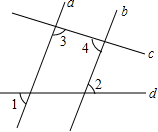 如图,∠1=65°,∠2=65°,∠3=95°
如图,∠1=65°,∠2=65°,∠3=95°