Question

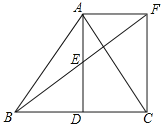
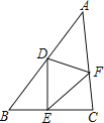
【题目】已知：如图，△ABC中，∠A=45°，AB=6，AC=，点D、E、F分别是三边AB、BC、CA上的点，则△DEF周长的最小值是______．

Answer 1

【答案】

【解析】

如图，作E关于AB的对称点，作E关于AC的对称点N，连接AE，MN，MN交AB于D，交AC于F，作AH⊥BC于H，CK⊥AB于K．由对称性可知：DE=DM，FE=FN，AE=AM=AN，推出△DEF的周长DE+EF+FD=DM+DF+FN，推出当点E固定时，此时△DEF的周长最小，再证明△MNA是等腰直角三角形，推出MN=AE，推出当AE的值最小时，MN的值最小，求出AE的最小值即可解决问题；

解：如图，作E关于AB的对称点，作E关于AC的对称点N，连接AE，MN，MN交AB于D，交AC于F，作AH⊥BC于H，CK⊥AB于K．

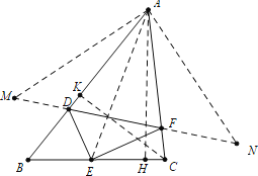
由对称性可知：DE=DM，FE=FN，AE=AM=AN，

∴△DEF的周长DE+EF+FD=DM+DF+FN，

∴当点E固定时，此时△DEF的周长最小，

∵∠BAC=45°，∠BAE=∠BAM，∠CAE=∠CAN，

∴∠MAN=90°，

∴△MNA是等腰直角三角形，

∴MN=AE，

∴当AE的值最小时，MN的值最小，

∵AC=4，

∴AK=KC=4，

∵AB=6，

∴BK=AB-AK=2，

在Rt△BKC中，∵∠BKC=90°，BK=2，CK=4，

∴BC==2，

∵BCAH=ABCK，

∴AH=，

根据垂线段最短可知：当AE与AH重合时，AE的值最小，最小值为，

∴MN的最小值为，

∴△DEF的周长的最小值为．

故答案为．