题目内容
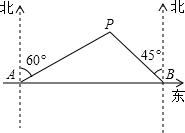 (2012•铁岭)如图,在东西方向的海岸线上有A、B两个港口,甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,问乙货船每小时航行
(2012•铁岭)如图,在东西方向的海岸线上有A、B两个港口,甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,问乙货船每小时航行2
| 2 |
2
海里.| 2 |
分析:作PC⊥AB于点C,首先在直角三角形APC中求得PC,然后在直角三角形中求得PB的长,最后除以时间即可得到乙货轮航行的速度.
解答: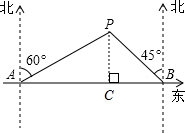 解:作PC⊥AB于点C,
解:作PC⊥AB于点C,
∵甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,
∴∠PAC=30°,AP=4×2=8,
∴PC=AP×sin30°=8×
=4.
∵乙货船从B港沿西北方向出发,
∴∠PBC=45°,
∴PB=PC÷
=4
,
∴乙货船每小时航行4
÷2=2
海里/小时,
故答案为2
.
 解:作PC⊥AB于点C,
解:作PC⊥AB于点C,∵甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,
∴∠PAC=30°,AP=4×2=8,
∴PC=AP×sin30°=8×
| 1 |
| 2 |
∵乙货船从B港沿西北方向出发,
∴∠PBC=45°,
∴PB=PC÷
| ||
| 2 |
| 2 |
∴乙货船每小时航行4
| 2 |
| 2 |
故答案为2
| 2 |
点评:本题考查了解直角三角形的应用,解题的关键是从纷杂的实际问题中整理出直角三角形并利用解直角三角形的知识求解.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
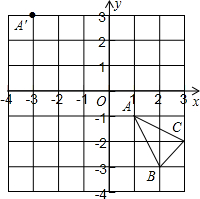 (2012•铁岭)如图,在平面直角坐标系中,△ABC经过平移后点A的对应点为点A′,则平移后点B的对应点B′的坐标为
(2012•铁岭)如图,在平面直角坐标系中,△ABC经过平移后点A的对应点为点A′,则平移后点B的对应点B′的坐标为 (2012•铁岭)如图,点E、F、G、H分别为菱形A1B1C1D1各边的中点,连接A1F、B1G、C1H、D1E得四边形A2B2C2D2,以此类推得四边形A3B3C3D3…,若菱形A1B1C1D1的面积为S,则四边形AnBnCnDn的面积为
(2012•铁岭)如图,点E、F、G、H分别为菱形A1B1C1D1各边的中点,连接A1F、B1G、C1H、D1E得四边形A2B2C2D2,以此类推得四边形A3B3C3D3…,若菱形A1B1C1D1的面积为S,则四边形AnBnCnDn的面积为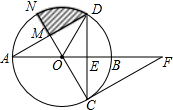 (2012•铁岭)如图,AB为⊙O的直径,弦CD垂直平分OB于点E,点F在AB延长线上,∠AFC=30°.
(2012•铁岭)如图,AB为⊙O的直径,弦CD垂直平分OB于点E,点F在AB延长线上,∠AFC=30°.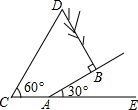 (2012•铁岭)如图,在斜坡AB上有一棵树BD,由于受台风影响而倾斜,恰好与坡面垂直,在地面上C点处测得树顶部D的仰角为60°,测得坡角∠BAE=30°,AB=6米,AC=4米.求树高BD的长是多少米?(结果保留根号)
(2012•铁岭)如图,在斜坡AB上有一棵树BD,由于受台风影响而倾斜,恰好与坡面垂直,在地面上C点处测得树顶部D的仰角为60°,测得坡角∠BAE=30°,AB=6米,AC=4米.求树高BD的长是多少米?(结果保留根号)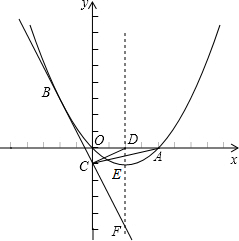 -2x-1经过抛物线上一点B(-2,m)且与y轴交于点C,与抛物线的对称轴交于点F.
-2x-1经过抛物线上一点B(-2,m)且与y轴交于点C,与抛物线的对称轴交于点F.