题目内容
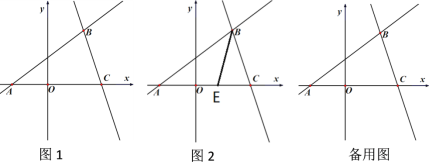
【题目】如图1,在平面直角坐标系中,直线![]() :
:![]() 与
与![]() 轴交于点A,且经过点B(2,m),点C(3,0).
轴交于点A,且经过点B(2,m),点C(3,0).
(1)求直线BC的函数解析式;
(2)在线段BC上找一点D,使得△ABO与△ABD的面积相等,求出点D的坐标;
(3)y轴上有一动点P,直线BC上有一动点M,若△APM是以线段AM为斜边的等腰直角三角形,求出点M的坐标;
(4)如图2,E为线段AC上一点,连结BE,一动点F从点B出发,沿线段BE以每秒1个单位运动到点E,再沿线段EA以每秒![]() 个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值.
个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() ;(4) t最小值为
;(4) t最小值为![]() 秒
秒
【解析】
(1)把B(2,m)代入直线l解析式可求出m的值,即可得B点坐标,设直线BC的解析式为y=kx+b,把B、C两点坐标代入可求得k、m的值,即可的直线BC的解析式;(2)过点O作![]() 交BC于点D,可知S△ABC=S△ABD,
交BC于点D,可知S△ABC=S△ABD,![]() ,联立直线BC与OD的解析式解得交点D的坐标即可;(3)分别讨论P点在y轴的负半轴和正半轴时两种情况,①P点在y轴的负半轴时,作
,联立直线BC与OD的解析式解得交点D的坐标即可;(3)分别讨论P点在y轴的负半轴和正半轴时两种情况,①P点在y轴的负半轴时,作![]() 于点N,可证明△AOP
于点N,可证明△AOP![]() △PNM1,设
△PNM1,设
OP=NM1=m,ON=m-2,则M1的坐标为(m,2-m),代入BC解析式即可求出m的值,进而可得M1坐标;②当P点在y轴正半轴时,同①解法可求出M2的坐标,综上即可得答案;(4)作射线AQ与x轴正半轴的夹角为45°,过点B作x轴的垂线交射线AQ于点Q,作![]() 于点K,作
于点K,作![]() 于点T,可求出AG、AQ、BQ的长,根据时间t=
于点T,可求出AG、AQ、BQ的长,根据时间t=![]() +
+![]() =BE+EK≥BT,利用面积法求出BT的值即可.
=BE+EK≥BT,利用面积法求出BT的值即可.
(1)解:将点B(2,m)代入![]() 得m=3
得m=3
∴![]()
设直线BC解析式为![]() 得到
得到![]()
∴![]()
∴直线BC解析式为![]()
( 2 )如图,过点O作![]() 交BC于点D
交BC于点D
∴S△ABC=S△ABD,![]()
∴直线OD的解析式为y=![]() x,
x,
∴
解得

![]()
(3)①如图,当P点在y轴负半轴时,作![]() 于点N,
于点N,
∵直线AB与x轴相交于点A,
∴点A坐标为(-2,0),
∵∠APO+∠PAO=90°,∠APO+∠PNM1=90°
∴∠PAO=∠PNM1,
又∵AP=PM1,∠POA=∠PNM1=90°
∴△AOP![]() △PNM1,
△PNM1,
∴PN=OA=2,
设OP=NM1=m,ON=m-2
∴![]()
解得![]()
![]() ∴
∴![]()

②如图,作![]() 于点H
于点H
可证明△AOP![]() △PHM2
△PHM2
设HM2=n,OH=n-2
∴![]()
解得![]()
∴M2(![]() ,
,![]() )
)

∴综上所述![]() 或M2(
或M2(![]() ,
,![]() ).
).
(4)如图,作射线AQ与x轴正半轴的夹角为45°,过点B作x轴的垂线交射线AQ于点Q,作![]() 于点K,作
于点K,作![]() 于点T,
于点T,
∵∠CAQ=45°BG⊥x轴,B(2,3)
∴AG=4,
∴AQ=4![]() ,BQ=7,
,BQ=7,
t=![]() =BE+EK≥BT,
=BE+EK≥BT,
由面积法可得:![]()
∴![]() ×4
×4![]() ×BT=
×BT=![]() ×7×4,
×7×4,
∴BT=![]()
因此t最小值为![]() .
.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案