题目内容
【题目】如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF的两边相交于A、B和C、D,连接OA,此时有OA∥PE. 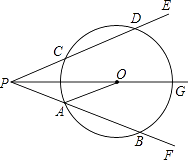
(1)求证:AP=AO;
(2)若tan∠OPB= ![]() ,求弦AB的长;
,求弦AB的长;
(3)若以图中已标明的点(即P、A、B、C、D、O)构造四边形,则能构成菱形的四个点为 , 能构成等腰梯形的四个点为或或 .
【答案】
(1)证明:∵PG平分∠EPF,
∴∠DPO=∠BPO,
∵OA∥PE,
∴∠DPO=∠POA,
∴∠BPO=∠POA,
∴PA=OA
(2)解:过点O作OH⊥AB于点H,则AH=HB= ![]() AB,
AB,

∵tan∠OPB= ![]() ,∴PH=2OH,
,∴PH=2OH,
设OH=x,则PH=2x,
由(1)可知PA=OA=10,∴AH=PH﹣PA=2x﹣10,
∵AH2+OH2=OA2,∴(2x﹣10)2+x2=102,
解得x1=0(不合题意,舍去),x2=8,
∴AH=6,∴AB=2AH=12
(3)P、A、O、C;A、B、D、C;P、A、O、D;P、C、O、B
【解析】(3)解:P、A、O、C;A、B、D、C或P、A、O、D或P、C、O、B. (1)由已知条件“射线PG平分∠EPF”求得∠DPO=∠BPO;然后根据平行线的性质,两直线OA∥PE,内错角∠DPO=∠POA;最后由等量代换知∠BPO=∠POA,从而根据等角对等边证明AP=AO;(2)设OH=x,则PH=2x.作辅助线OH(“过点O作OH⊥AB于点H”),根据垂径定理知AH=HB= ![]() AB;又由已知条件“tan∠OPB=
AB;又由已知条件“tan∠OPB= ![]() ”求得PH=2OH;然后利用(1)的结果及勾股定理列出关于x的一元二次方程,解方程即可;(3)根据菱形的性质、等腰梯形的判定定理填空.
”求得PH=2OH;然后利用(1)的结果及勾股定理列出关于x的一元二次方程,解方程即可;(3)根据菱形的性质、等腰梯形的判定定理填空.

 阅读快车系列答案
阅读快车系列答案【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
(1)根据图示填写下表:
平均数/分 | 中位数/分 | 众数/分 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.






