Question

（本题10分）如图，点E是矩形ABCD中CD边上一点，△BCE沿BE折叠为△BFE，点F落在AD上。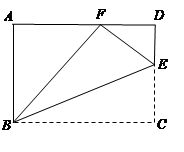

（1）求证：△ABF∽△DFE；
（2）若△BEF∽△ABF，求CD∶BC的值。

Answer 1

（1）在矩形ABCD中，∠A＝∠D＝90°，
又∠ABF＝∠DFE，
∴△ABF∽△DFE
（2）∵AD∥BC，∴∠AFB=FBC，又∠FBE=∠CBE，由已知条件知△BEF∽△ABF，∴∠AFB=∠FEB，∴∠FEB=2∠FBE，又∠BFE=90°，∴∠FBE=30°，∴∠EBC=30°，∵△BFE≌△BCE，∴BF=BC，∵∠FBC=60°，∴△BCF为等边三角形，另BC=x，∴CF=x，CD=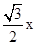，∴CD:BC=。

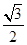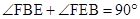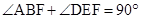解析试题分析：（1）因为∠ABE+∠DEB=90°，又，所以，可推出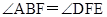，从而推出两三角形相似。
（2）又内错角相等，推出图中四个三角形都为直角三角形且其中一个角为30°，又根据两边相等且顶角为60°的三角形为等边三角形，从而可以化出CD与BC的关系式。
考点：相似三角形；全等三角形
点评：利用相似三角形各组角相等，全等三角形各组边相等，可以将题目简单化，进而求出正确答案。