题目内容
若关于x的一元二次方程x2+kx+4k2-3=0的两个实数根分别是x1,x2,且满足x1+x2=x1•x2.则k的值为
- A.-1或

- B.-1
- C.

- D.不存在
C
分析:根据一元二次方程根与系数的关系及x1+x2=x1x2,得出关于k的方程,解方程并用根的判别式检验得出k的值即可.
解答:由根与系数的关系,得x1+x2=-k,
因为x1x2=4k2-3,又x1+x2=x1x2,
所以-k=4k2-3,即4k2+k-3=0,
解得k= 或-1,
或-1,
因为△≥0时,所以k2-4(4k2-3)≥0,
解得: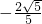 ≤k≤
≤k≤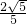 ,故k=-1舍去,
,故k=-1舍去,
∴k= .
.
故选C.
点评:本题主要考查了一元二次方程根与系数关系的应用,属于基础题,关键不要忘记利用根的判别式进行检验.
分析:根据一元二次方程根与系数的关系及x1+x2=x1x2,得出关于k的方程,解方程并用根的判别式检验得出k的值即可.
解答:由根与系数的关系,得x1+x2=-k,
因为x1x2=4k2-3,又x1+x2=x1x2,
所以-k=4k2-3,即4k2+k-3=0,
解得k=
 或-1,
或-1,因为△≥0时,所以k2-4(4k2-3)≥0,
解得:
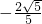 ≤k≤
≤k≤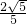 ,故k=-1舍去,
,故k=-1舍去,∴k=
 .
.故选C.
点评:本题主要考查了一元二次方程根与系数关系的应用,属于基础题,关键不要忘记利用根的判别式进行检验.

练习册系列答案
相关题目