Question

已知：如图，在平面直角坐标系中，半径为2

2

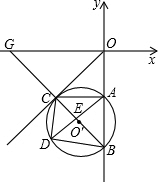的⊙O′与y轴交于A、B两点，与直线OC相切于点C，∠BOC=45°，BC⊥OC，垂足为C．
（1）判断△ABC的形状；
（2）在

BC

上取一点D，连接DA、DB、DC，DA交BC于点E．求证：BD•CD=AD•ED；
（3）延长BC交x轴于点G，求经过O、C、G三点的二次函数的解析式．

Answer 1

分析：（1）由于OC是圆的切线，而BC⊥OC，那么BC必过圆心，也就是说BC为圆O′的直径，那么∠CAB=90°，即三角形BAC是直角三角形，又由∠BOC=45°，那么∠CBO=45°，因此三角形BAC是等腰直角三角形．
（2）本题其实证的是三角形ADC和BDE相似，这两个三角形中，根据圆周角定理可得出∠CAD=∠DBE，根据（1）的结论又能得出弧AC=弧AB，那么可得出∠ADC=∠BDE，由此可得出两三角形相似，也就能得出本题要证得结论．
（3）已知了半径的长，就能求出CA，OA的长，也就知道了C的坐标，知道OA，CA，AB的长也就能求出OB的长，又因为三角形OGB也是个等腰直角三角形因此OG=OB，可得出G的坐标，然后用待定系数法即可得出过O，C，G的二次函数的解析式．

解答：（1）解：∵OC与⊙O'相切
∴O'C⊥OC
又∵BC⊥OC
∴O'在BC上，即BC为⊙O'的直径
∴∠CAB=90°
∴CA⊥BA
∵∠BOC=45°
∴△BOC为等腰直角三角形
∴A为OB的中点，CD=

1

2

OB=AB
∴△ABC是等腰直角三角形．

（2）证明：∵AC=AB
∴

AC

=

AB

．
∴∠ADC=∠ADB
又∵∠CAD=∠CBD
∴△ADC∽△BDE
∴

AD

BD

=

DC

DE

，
即BD•CD=AD•ED．

（3）解：在Rt△BOC中
∵⊙O′的半径为2

2

∴BC=4

2

∵∠BOC=45°
∴OB=

2

•BC=8，CA=OA=AB=

1

2

OB=4
∵CA∥x轴，
∴C点坐标为（-4，-4）
∴BC=CG
∴AC为△BGO的中位线
∴OG=2AC=8
∴G点坐标为（-8，0）
设过O、C、G三点的二次函数为y=ax²+bx+c，
由已知，函数图象过（0，0），（-4，-4），（-8，0）三点，得

c=0 16a-4b=-4 64a-8b=0

解这个方程组，得
a=

1

4

，b=2，c=0
因此，所求二次函数是y=

1

4

x²+2x．

点评：本题主要考查了等腰直角三角形的性质，相似三角形的判定以及二次函数的综合应用等知识．根据等腰三角形的性质得出相关的线段相等是解题的关键．