Question

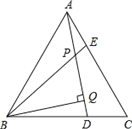
【题目】如图，△ABC是等边三角形，AE=CD，BQ⊥AD于Q，BE交AD于P．

（1）求证：△ABE≌△CAD；

（2）求∠PBQ的度数．

Answer 1

【答案】（1）见解析；（2）30o

【解析】试题分析：（1）由等边三角形的性质可得AB=AC，∠BAC=∠C=60°，然后利用“边角边”即可证明两三角形；
（2）由SAS可得△ABE≌△CAD，进而得出对应角相等，再通过角之间的转化即可求解∠BPD的度数，进而求得结论．

试题解析：

∵△ABC是等边三角形，
∴AB=AC，∠BAC=∠C=60°，
在△ABE与△CAD中，

∴△ABE≌△CAD（SAS）；
（2）由（1）知△ABE≌△CAD，
∴∠ABE=∠CAD，
∴∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°．
∴∠PBQ=90°-∠BPQ=30°．