题目内容
若⊙O1和⊙O2相交于A、B两点,⊙O1和⊙O2的半径分别为2和| 2 |
分析:连接AB、O1O2,两线段交于点C,由垂径定理可得:O1O2⊥AB且平分AB,再解Rt△O1CA、Rt△O2CA,可得∠O1AC、∠O2AC,即可求得∠O1AO2的度数.
解答: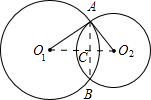 解:连接AB、O1O2,两线段交于点C,如下图所示:
解:连接AB、O1O2,两线段交于点C,如下图所示:
①∵AB为两圆的交线,O1O2为两圆圆心的连线,
∴O1O2⊥AB且平分AB;
∵已知O1A=2,O2A=
,AB=2,
∴在Rt△O1CA中,cos∠O1AC=
,
∴∠O1AC=60°;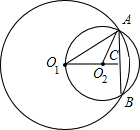
在Rt△O2CA中,cos∠O2AC=
,
∴∠O2AC=45°,
∴∠O1AO2=∠O1AC+∠O2AC=105°,
②当如图所示:
同理可得:∴∠O1AO2=∠O1AC-∠O2AC=15°,
故此题应该填105°或15°.
 解:连接AB、O1O2,两线段交于点C,如下图所示:
解:连接AB、O1O2,两线段交于点C,如下图所示:①∵AB为两圆的交线,O1O2为两圆圆心的连线,
∴O1O2⊥AB且平分AB;
∵已知O1A=2,O2A=
| 2 |
∴在Rt△O1CA中,cos∠O1AC=
| 1 |
| 2 |
∴∠O1AC=60°;

在Rt△O2CA中,cos∠O2AC=
| ||
| 2 |
∴∠O2AC=45°,
∴∠O1AO2=∠O1AC+∠O2AC=105°,
②当如图所示:
同理可得:∴∠O1AO2=∠O1AC-∠O2AC=15°,
故此题应该填105°或15°.
点评:本题主要考查了相交圆的性质及直角三角形的性质.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目