题目内容
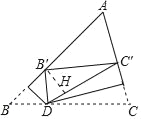
【题目】如图，一张三角形纸片ABC，其中∠BAC=60°，BC=6，点D是BC边上一动点，将BD，CD翻折使得B′，C′分别落在AB，AC边上，（B与B′，C与C′分别对应），点D从点B运动至点C，△B′C′D面积的大小变化情况是（ ）
A. 一直减小 B. 一直不变 C. 先减小后增大 D. 先增大后减小
【答案】D
【解析】
作B′H⊥DC′于H．设BD=DB′=x，则CD=DC′=6﹣x．由折叠得性质可求出∠B′DC′=60°，从而利用锐角三角函数知识表示出B′H的值，然后根据三角形的面积公式列出函数关系式解答即可.
如图，作B′H⊥DC′于H．设BD=DB′=x，则CD=DC′=6﹣x．
∵∠A=60°，
∴∠B+∠C=120°，
由翻折不变性可知：∠B=∠DB′B，∠C=∠DC′C，
∴∠BDB′+∠CDC′=120°，
∴∠B′DC′=60°，
∴B′H=sin60x=
x，
∴S△DB′C′=
x（6﹣x）=﹣
（x﹣3）2+
，
∴S△DB′C′的值先增大后减小，
故选：D．
【题目】深圳市某校艺术节期间，开展了“好声音”歌唱比赛，在初赛中，学生处对初赛成绩做了统计分析，绘制成如下频数、频率分布表和频数分布直方图（如图），请你根据图中提供的信息，解答下列问题：
分组 | 频数 | 频率 |
74.5≤x＜79.5 | 2 | 0.04 |
79.5≤x＜84.5 | a | 0.16 |
84.5≤x＜89.5 | 20 | 0.40 |
89.5≤x＜94.5 | 16 | 0.32 |
94.5≤x＜100.5 | 4 | b |
合计 | 50 | 1 |
（1）频数、频率分布表中a= ，b= ；
（2）补全频数分布直方图；
（3）初赛成绩在94.5≤x＜100.5分的四位同学恰好是七年级、八年级各一位，九年级两位，学生处打算从中随机挑选两位同学谈一下决赛前的训练，则所选两位同学恰好都是九年级学生的概率为 ．
