题目内容
某校为了了解九年级学生的体能素质，在400名学生中随机选择部分学生进行测试，其中一项为立定跳远．有关数据整理如下：| 立定跳远成绩（分） | 学生人数（人） |
| 10 | m |
| 9 | 16 |
| 8 | 4 |
| 7 | n |
| 6 | |
| 5 | 2 |
| 合计 |
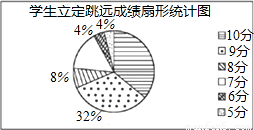
（2）在扇形统计图（如图）中表示立定跳远成绩为8分的扇形圆心角的度数为______°（精确到1°）；
（3）已知测试成绩为10分的学生比成绩为7分的学生多10人，求m和n的值．
【答案】分析：（1）用立定跳远成绩为9分的学生人数除以立定跳远成绩为9分的学生人数所占的百分比，即可求出样本容量；
（2）用立定跳远成绩为8分的学生人数所占的百分比乘以360°即可求出答案．
（3）先求出测试成绩为10分的学生和成绩为7分的学生之和，再根据测试成绩为10分的学生比成绩为7分的学生多10人，列出方程组，即可求出m，n的值．
解答：解：（1）由统计表得：样本总量为：16÷32%=50；
（2）立定跳远成绩为8分的扇形圆心角的度数为：360°×8%≈29°；
（3）根据题意，得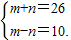
解方程组，得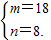
答：m=18，n=8．
故答案为；50，29．
点评：本题考查了统计表、扇形统计图、以及用样本估计总体的知识，此题综合性较强，但难度适中，易于掌握．
（2）用立定跳远成绩为8分的学生人数所占的百分比乘以360°即可求出答案．
（3）先求出测试成绩为10分的学生和成绩为7分的学生之和，再根据测试成绩为10分的学生比成绩为7分的学生多10人，列出方程组，即可求出m，n的值．
解答：解：（1）由统计表得：样本总量为：16÷32%=50；
（2）立定跳远成绩为8分的扇形圆心角的度数为：360°×8%≈29°；
（3）根据题意，得
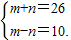
解方程组，得
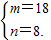
答：m=18，n=8．
故答案为；50，29．
点评：本题考查了统计表、扇形统计图、以及用样本估计总体的知识，此题综合性较强，但难度适中，易于掌握．
练习册系列答案
名校课堂系列答案
相关题目
15、某校为了了解九年级学生的体能情况，随机抽查了其中的30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图的频数分布直方图，则仰卧起坐次数在20～25次之间的频数是
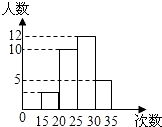某校为了了解九年级学生的体能情况，随机抽查了其中的30名学生，测试了1分钟仰卧起座的次数，并绘制成如图所示的频数分布直方图，请根据图示计算，仰卧起座次数在15～20次之间的频率是（ ）| A、0.1 | B、0.17 | C、0.33 | D、0.4 |
某校为了了解九年级学生的体能情况，抽调了一部分学生进行一分钟跳绳测试，将测试成绩整理后作出如下统计图．甲同学计算出前两组的频率和是0.12，乙同学计算出跳绳次数不少于100次的同学占96%，丙同学计算出从左至右第二、三、四组的频数比为4：17：15，统计图如图所示，则本次测试共抽调人数为（ ）
（2007•海淀区二模）某校为了了解九年级学生的体能素质，在400名学生中随机选择部分学生进行测试，其中一项为立定跳远．有关数据整理如下：
某校为了了解九年级学生的体能情况，抽调了一部分学生进行一分钟跳绳测试，将测试成绩整理后作出如下统计图．甲同学计算出第二组的频率是0.08，乙同学计算出从左至右第一、二、三、四组的频数比为2：4：17：15．结合统计图回答下列问题：