题目内容
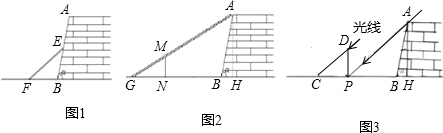
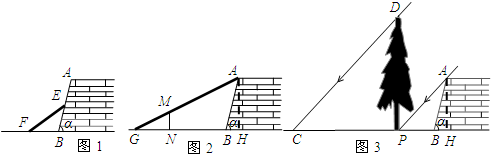
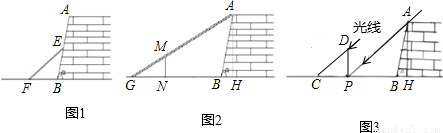
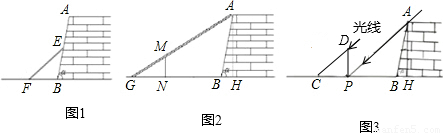
九(1)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,使长方形框架面积最大.小组讨论后,同学们做了以下三种试验:

请根据以上图案回答下列问题:
(1)在图案①中,如果铝合金材料总长度(图中所有黑线的长度和)为6 m,当AB为1 m,长方形框架ABCD的面积是__________m2;
(2)在图案②中,如果铝合金材料总长度为6 m,设AB为x m,长方形框架ABCD?的面积为S=________(用含x的代数式表示);当AB=_______m时,长方形框架ABCD的面积S最大;
在图案③中,如果铝合金材料总长度为l m,设AB为x m,当AB=________m时,长方形框架ABCD的面积S最大.
(3)经过这三种情形的试验,他们发现对于图案④这样的情形也存在着一定的规律.
探索:如图案④,如果铝合金材料总长度为l m共有n条竖档时,那么当竖档AB多少时,长方形框架ABCD的面积最大.
答案:
解析:
解析:
|
思路解析:用函数考虑.当AB为x m,列出面积的表达式,构成方程或函数,用它们的性质解决问题.
(1)图案①中,当AB为1 m时,AD=(6-1×2)÷3= (2)图案②中,当AB为x(0<X2+2x,当x=1时,S有最大值. 图案③中,当AB为x(0<X< (3)图案④中,当AB为x(0<X< 解:(1) (3)设AB长为x m,那么AD为 S=x· 当 |

练习册系列答案
相关题目