Question

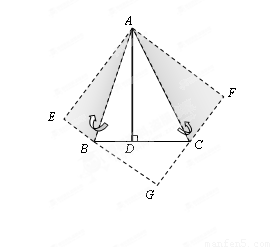
已知α＞45°，下列各式：tanα、sinα、cosα由小到大排列为（　　）

• A、tanα＜sinα＜cosα
• B、cosα＜tanα＜sinα
• C、cosα＜sinα＜tanα
• D、sinα＜cosα＜tanα

Answer 1

分析：画出图形，设∠A=α＞45°，∠C=90°，求出tanα=

a

b

，sinα=

a

c

，cosα=

b

c

，根据

a

b

＞

a

c

＞

b

c

，求出即可．

解答：解：设∠A=α＞45°，∠C=90°，
∴∠B=90°-∠A＜45°＜∠A，
∴b＜a＜c，
∵tanα=tanA=

a

b

，sinα=sinA=

a

c

，cosα=cosA=

b

c

，
∵

a

b

＞

a

c

＞

b

c

，
tanα＞sinα＞cosα，
故选C．

点评：本题考查了锐角三角函数的定义和锐角三角函数的增减性的应用，根据是求出tanα=

a

b

、sinα=

a

c

、cosα=

b

c

和得出不等式

a

b

＞

a

c

＞

b

c

．