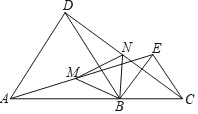
题目内容
【题目】(2013年浙江义乌10分)小明合作学习小组在探究旋转、平移变换.如图△ABC,△DEF均为等腰直角三角形,各顶点坐标分别为A(1,1),B(2,2),C(2,1),D(![]() ,0),E(
,0),E(![]() , 0),F(
, 0),F(![]() ,
,![]() ).
).
(1)他们将△ABC绕C点按顺时针方向旋转450得到△A1B1C.请你写出点A1,B1的坐标,并判断A1C和DF的位置关系;
(2)他们将△ABC绕原点按顺时针方向旋转450,发现旋转后的三角形恰好有两个顶点落在抛物线![]() 上.请你求出符合条件的抛物线解析式;
上.请你求出符合条件的抛物线解析式;
(3)他们继续探究,发现将△ABC绕某个点旋转45,若旋转后的三角形恰好有两个顶点落在抛物线![]() 上,则可求出旋转后三角形的直角顶点P的坐标.请你直接写出点P的所有坐标.
上,则可求出旋转后三角形的直角顶点P的坐标.请你直接写出点P的所有坐标.

【答案】解:(1)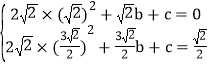 。
。
A1C和DF的位置关系是平行。
(2)∵△ABC绕原点按顺时针方向旋转45°后的三角形即为△DEF,
∴①当抛物线经过点D、E时,根据题意可得: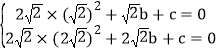 ,解得
,解得![]() 。
。
∴![]() 。
。
②当抛物线经过点D、F时,根据题意可得: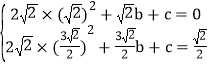 ,解得
,解得![]() 。
。
∴![]() 。
。
③当抛物线经过点E、F时,根据题意可得: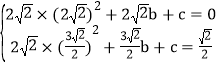 ,解得
,解得![]() 。
。
∴![]() 。
。
(3)在旋转过程中,可能有以下情形:
①顺时针旋转45°,点A、B落在抛物线上,如答图1所示,
易求得点P坐标为(0,![]() )。
)。
②顺时针旋转45°,点B、C落在抛物线上,如答图2所示,
设点B′,C′的横坐标分别为x1,x2,
易知此时B′C′与一、三象限角平分线平行,∴设直线B′C′的解析式为y=x+b。
联立y=x2与y=x+b得:x2=x+b,即![]() ,∴
,∴![]() 。
。
∵B′C′=1,∴根据题意易得:![]() ,∴
,∴![]() ,即
,即![]() 。
。
∴![]() ,解得
,解得![]() 。
。
∴![]() ,解得
,解得![]() x或
x或![]() 。
。
∵点C′的横坐标较小,∴![]() 。
。
当![]() 时,
时,![]() 。
。
∴P(![]() ,
,![]() )。
)。
③顺时针旋转45°,点C、A落在抛物线上,如答图3所示,
设点C′,A′的横坐标分别为x1,x2.
易知此时C′A′与二、四象限角平分线平行,∴设直线C′A′的解析式为![]() 。
。
联立y=x2与![]() 得:
得:![]() ,即
,即![]() ,∴
,∴![]() 。
。
∵C′A′=1,∴根据题意易得:![]() ,∴
,∴![]() ,即
,即![]() 。
。
∴![]() ,解得
,解得![]() 。
。
∴![]() ,解得
,解得![]() x或
x或![]() 。
。
∵点C′的横坐标较大,∴![]() 。
。
当![]() 时,
时,![]() 。
。
∴P(![]() ,
,![]() )。
)。
④逆时针旋转45°,点A、B落在抛物线上.
因为逆时针旋转45°后,直线A′B′与y轴平行,因为与抛物线最多只能有一个交点,故此种情形不存在。
⑤逆时针旋转45°,点B、C落在抛物线上,如答图4所示,
与③同理,可求得:P(![]() ,
,![]() )。
)。
⑥逆时针旋转45°,点C、A落在抛物线上,如答图5所示,
与②同理,可求得:P(![]() ,
,![]() )。
)。
综上所述,点P的坐标为:(0,![]() ),(
),(![]() ,
,![]() ),P(
),P(![]() ,
,![]() ,(
,(![]() ,
,![]() )。
)。

【解析】
(1)由旋转性质及等腰直角三角形边角关系求解。
(2)首先明确△ABC绕原点按顺时针方向旋转45°后的三角形即为△DEF,然后分三种情况进行讨论,分别计算求解。
(3)旋转方向有顺时针、逆时针两种可能,落在抛物线上的点有点A和点B、点B和点C、点C和点D三种可能,因此共有六种可能的情形,需要分类讨论,避免漏解。

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 278 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计当![]() 很大时,摸到白球的频率将会接近 (精确到0.1);
很大时,摸到白球的频率将会接近 (精确到0.1);
(2)假如摸一次,摸到黑球的概率![]() ;
;
(3)试估算盒子里黑颜色的球有多少只.