Question

【题目】如图所示，在四边形中，，分别是的中点，，则的长是___________.

Answer 1

【答案】

【解析】

根据中位线定理和已知，易证明△PMN是等腰三角形，根据等腰三角形的性质和已知条件即可求出∠PMN的度数为30°，通过构造直角三角形求出MN．

解：∵在四边形ABCD中，M、N、P分别是AD、BC、BD的中点，
∴PN，PM分别是△CDB与△DAB的中位线，
∴PM=AB=2，PN=DC=2，PM∥AB，PN∥DC，
∵AB=CD，
∴PM=PN，
∴△PMN是等腰三角形，
∵PM∥AB，PN∥DC，
∴∠MPD=∠ABD=20°，∠BPN=∠BDC=80°，
∴∠MPN=∠MPD+∠NPD=20°+（180-80）°=120°，
∴∠PMN==30°．

过P点作PH⊥MN，交MN于点H．

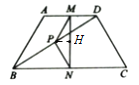
∵HQ⊥MN，
∴HQ平分∠MHN，NH=HM．
∵MP=2，∠PMN=30°，
∴MH=PMcos60°=，
∴MN=2MH=2．