题目内容
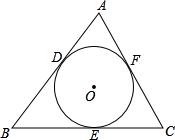如图，⊙O与△ABC的边BC、AC、AB分别切于E、F、D三点，若⊙O的半径是1，∠C=60°，AB=5，则△ABC的周长为分析：此题根据切线长定理，得AF=AD，BE=BD，CE=CF．要求三角形ABC的周长，只需求得CE的长，连接OC，OE．根据切线的性质定理，得OE⊥BC；最后根据切线长定理，得∠OCE=30°，先求CE，OE的长，从而求得△ABC的周长．
解答：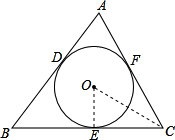
解：连接OC，OE，
∵⊙O与△ABC的边BC、AC、AB分别切于E、F、D三点，
∴AD=AF，CE=CF，BD=BE，
∵OE=1，∠C=60°，
∴∠OCE=30°，
∴CE=
，OE=1，
∴CE+CF=2
，
∴AD+BD=AF+BE=AB=5，
∴AB+BE+AF=10，
∴△ABC的周长为10+2
．
解：连接OC，OE，∵⊙O与△ABC的边BC、AC、AB分别切于E、F、D三点，
∴AD=AF，CE=CF，BD=BE，
∵OE=1，∠C=60°，
∴∠OCE=30°，
∴CE=
| 3 |
∴CE+CF=2
| 3 |
∴AD+BD=AF+BE=AB=5，
∴AB+BE+AF=10，
∴△ABC的周长为10+2
| 3 |
点评：此题考查了切线长定理，能够熟练运用锐角三角函数进行计算．
练习册系列答案
相关题目
如图，DE与△ABC的边AB、AC分别相交于D、E两点，且DE∥BC．若DE=2cm，BC=3cm，EC=
25、如图，作出与△ABC关于y轴对称的图形，并写出相应顶点的坐标．
（2009•自贡）如图，⊙O与△ABC中AB、AC的延长线及BC边相切，且∠ACB=90°，∠A，∠B，∠C所对的边长依次为3，4，5，则⊙O的半径是