题目内容
某射手在一次射击中射中10环、9环、8环、7环、7环以下的概率分别为0.24、0.28、0.19、0.16、0.13.计算这个射手在一次射击中:
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数不足8环的概率.
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数不足8环的概率.
(1)0.52;(2)0.87;(3)0.29.
试题分析:(1)这个射手在一次射击中射中10环或9环,有两种情况,分别是射中10环和射中9环,把每种情况的概率求出,再相加即可.
(2)这个射手在一次射击中至少射中7环,有四种情况,分别为射中10环,射中9环,射中8环,射中7环,分别求出概率,再相加即可.也可用1减去对立事件的概率来求.
(3)这个射手在一次射击中射中环数不是8环,则为射中8环的对立事件,只要用1减去射中8环的概率即可.
设“射中10环”“射中9环”“射中8环”“射中7环”“射中7环以下”的事件分别为A、B、C、D、E,则
(1)P(A+B)=P(A)+P(B)=0.24+0.28=0.52,
即射中10环或9环的概率为0.52;
(2)P(A+B+C+D)=P(A)+P(B)+P(C)+P(D)=0.24+0.28+0.19+0.16=0.87,
即至少射中7环的概率为0.87;
(3)P(D+E)=P(D)+P(E)=0.16+0.13=0.29,
即射中环数不足8环的概率为0.29.
点评:解答本题的关键是掌握互斥事件有一个发生的概率公式的应用,若A,B互斥,则P(A+B)=P(A)+P(B),当一个事件的正面情况比较多或正面情况难确定时,常考虑对立事件.

练习册系列答案
相关题目
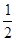 .
.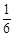
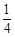
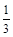
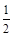
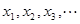
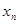 的平均数是2,方差是3,则另一组数据:
的平均数是2,方差是3,则另一组数据: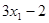 ,
,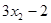 ,
,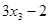 ,…
,…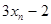 的平均数是 ,方差是 .
的平均数是 ,方差是 .