题目内容

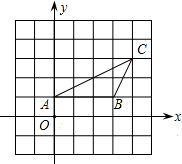
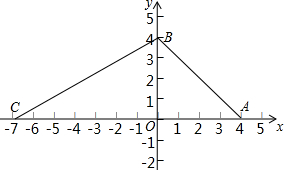
在平面直角坐标系中，△ABC的顶点A（4，0），B（0，4），点C在x轴的负半轴，且∠BCO=30°，BC=8，画出符合条件的图形，并求出点C的坐标及△ABC的面积S和周长C．
符合条件的图如下所示：
根据分析，设C点坐标是（a，0），则BC=
(a-0)2+(0-4)2
=8，解得：a1=4
3
（不合题意，舍去），a2=-4
3
，
即C点的坐标为：（-4
3
，0），
∴S=
1
2
×OB×OC+
1
2
×OA×OB=
1
2
×4×4
3
+
1
2
×4×4=8
3
+8，
∴C=BC+AC+AB=8+4
3
+4+4
2
=12+4
3
+4
2
．
练习册系列答案
相关题目
已知点A（1，3），B（3，2）．
（1）在如图所示边长为1的正方形网格中建立平面直角坐标系描出点A、B．
（2）求出△AOB的面积（其中O为坐标原点）
（3）设AB交x轴于点C，求C点的坐标．
（4）试在x轴上找一点D，使S△ADB=2S△AOB．
如图，△ABC中，点A的坐标为（0，1），点C的坐标为（4，3），如果要使△ABD与△ABC全等，那么点D的坐标是______．
如图所示，上，下两幅“娃娃脸”图案关于x轴对称，上图中左，右眼睛的坐标分别为（2.5，3），（3.5，3），则下图中左，右眼睛的坐标是______．
如图，点A的坐标为（-1，0），点B在直线y=x上运动，当线段AB最短时，点B的坐标为（　　）
A．（0，0）B．（
2
2
，-
2
2
）		C．（-
1
2
，-
1
2
）		D．（-
2
2
，-
2
2
）
如图的围棋盘放在平面直角坐标系内，黑棋A的坐标为（-1，2），那么白棋B的坐标是______．
已知：如图，A1（1，0），A2（1，1），A3（-1，1），A4（-1，-1），A5（2，-1）．
（1）继续填写：A6（______，______），A7（______，______），A8（______，______），A9（______，______）．A10（______，______），A11（______，______），A12（______，______），A13（______，______）．
（2）写出点A2010（______，______），A2011（______，______）．
已知点P在第四象限，且到x轴的距离为3，到y轴的距离为2，则点P的坐标一定是（　　）
A．（-2，3）B．（2，3）C．（-3，2）D．（2，-3）
已知∠α、∠β，线段a，求作△ABC，使BC=a，∠B=∠α，∠C=∠β．（要求：尺规作图，保留作图痕迹，不必写作法、证明）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网