题目内容
(2012•滨湖区模拟)“知识改变命运,科技繁荣祖国.”为提升中小学生的科技素养,我区每年都要举办中小学科技节.为迎接比赛,某校进行了宣传动员并公布了相关项目如下:A--杆身橡筋动力模型;B--直升橡筋动力模型;C--空轿橡筋动力模型.右图为该校报名参加科技比赛的学生人数统计图.

(1)该校报名参加B项目学生人数是
(2)该校报名参加C项目学生人数所在扇形的圆心角的度数是
(3)为确定参加区科技节的学生人选,该校在集训后进行了校内选拔赛,最后一轮复赛,决定在甲、乙2名候选人中选出1人代表学校参加区科技节B项目的比赛,每人进行了4次试飞,对照一定的标准,判分如下:甲:80,70,100,50;乙:75,80,75,70.如果你是教练,你打算安排谁代表学校参赛?请说明理由.

(1)该校报名参加B项目学生人数是
10
10
人;(2)该校报名参加C项目学生人数所在扇形的圆心角的度数是
119.988
119.988
°;(3)为确定参加区科技节的学生人选,该校在集训后进行了校内选拔赛,最后一轮复赛,决定在甲、乙2名候选人中选出1人代表学校参加区科技节B项目的比赛,每人进行了4次试飞,对照一定的标准,判分如下:甲:80,70,100,50;乙:75,80,75,70.如果你是教练,你打算安排谁代表学校参赛?请说明理由.
分析:(1)用参加A项目学生人数除以参加A项目学生人数所占的百分比即可求出参加科技比赛的总人数,用总人数乘以参加B项目学生人数所占的百分比即可,
(2)用360°乘以报名参加C项目学生人数所占的百分比即可,
(3)分别计算出甲、乙2名候选人的平均分和方差即可.
(2)用360°乘以报名参加C项目学生人数所占的百分比即可,
(3)分别计算出甲、乙2名候选人的平均分和方差即可.
解答: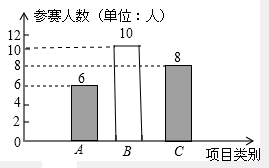 解:(1)∵参加科技比赛的总人数是6÷25%=24,
解:(1)∵参加科技比赛的总人数是6÷25%=24,
∴报名参加B项目学生人数是24×41.67%=10,
故答案为10;
(2)该校报名参加C项目学生人数所在扇形的圆心角的度数是360°×(1-25%-41.67%)=119.988°,
故答案为119.988;
(3)∵
=
=75,
∴S2甲=
[(80-75)2+(70-75)2+(100-75)2+(50-75)2]=325,
S2乙═
[(75-75)2+(80-75)2+(75-75)2+(70-75)2]=12.5,
∵S2甲>S2乙,
∴选乙.
 解:(1)∵参加科技比赛的总人数是6÷25%=24,
解:(1)∵参加科技比赛的总人数是6÷25%=24,∴报名参加B项目学生人数是24×41.67%=10,
故答案为10;
(2)该校报名参加C项目学生人数所在扇形的圆心角的度数是360°×(1-25%-41.67%)=119.988°,
故答案为119.988;
(3)∵
. |
| X甲 |
. |
| X乙 |
∴S2甲=
| 1 |
| 4 |
S2乙═
| 1 |
| 4 |
∵S2甲>S2乙,
∴选乙.
点评:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
 (2012•滨湖区模拟)如图,已知⊙O的半径为5,弦AB长为6,P为AB上一点(不含端点A和B),且OP长为整数,则OP长等于( )
(2012•滨湖区模拟)如图,已知⊙O的半径为5,弦AB长为6,P为AB上一点(不含端点A和B),且OP长为整数,则OP长等于( )