题目内容
【题目】如图，⊙C经过原点且与两坐标轴分别交于点A和点B，点A的坐标为(0，2)，D为⊙C在第一象限内的一点，且∠ODB＝60°.
(1)求⊙C的半径；
(2)求圆心C的坐标．
【答案】（1）2（2）（
，1）
【解析】试题分析：⑴ 根据同弧所对的圆周角度数相等可得∠AOB的度数，然后根据特殊角三角函数值可得直径AB的长，进而求得圆的半径长度.
(2)先利用勾股定理求出OB的长，再利用垂径定理求得OE、OF的长度，即可得到点C的坐标.
试题解析：⑴ 连接AB，如图所示，
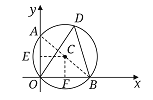
∵∠ AOB＝90°，∴ AB是⊙ C的直径．
∵∠ ODB＝60°，∴ ∠ OAB＝60°.
∵点A的坐标为(0，2)，∴ OA＝2.
在Rt△ AOB中，∠ OAB＝60°，∴ AB＝2OA＝4，∴ ⊙ C的半径为2.
(2)如上图所示，过点C坐CE⊥OA与点E，CF⊥OB与点F，则Rt△AOB中，由勾股定理可得，
，由垂径定理可知，
，
，又因为点C在第一象限，故圆心C的坐标为（ ，1）.
练习册系列答案
相关题目
