题目内容
【题目】在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F.且BD=BF. 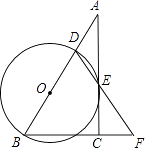
(1)求证:AC与⊙O相切.
(2)若BC=6,AB=12,求⊙O的面积.
【答案】
(1)证明:连接OE,
∵OD=OE,
∴∠ODE=∠OED,
∵BD=BF,
∴∠ODE=∠F,
∴∠OED=∠F,
∴OE∥BF,
∴∠AEO=∠ACB=90°,
∴AC与⊙O相切

(2)解:由(1)知∠AEO=∠ACB,又∠A=∠A,
∴△AOE∽△ABC,
∴ ![]() ,
,
设⊙O的半径为r,则 ![]() ,
,
解得:r=4,
∴⊙O的面积π×42=16π
【解析】(1)连接OE,求出∠ODE=∠F=∠DEO,推出OE∥BC,得出OE⊥AC,根据切线的判定推出即可;(2)证△AEO∽△ACB,得出关于r的方程,求出r即可.

练习册系列答案
相关题目