题目内容
求证:三角形的一边两端点到这边的中线的距离与到中线的延长线的距离相等.画图写出已知,求证并证明.
【答案】分析:此题首先利用已知条件证明△BED≌△CFD,再根据全等三角形的性质得以证明题目结论.
解答:已知:如图所示,AD为△ABC的中线,且CF⊥AD于F,BE⊥AD的延长线于E.
求证:BE=CF.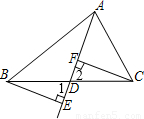
证明:∵AD为△ABC的中线.
∴BD=CD,
∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°,
又∠1=∠2,
∴△BED≌△CFD(AAS),
∴BE=CF.
(本题还可以作AN⊥BC于N,利用等底等高的两个三角形的面积相等的性质证明)
点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,同时掌握全等三角形的性质.
解答:已知:如图所示,AD为△ABC的中线,且CF⊥AD于F,BE⊥AD的延长线于E.
求证:BE=CF.

证明:∵AD为△ABC的中线.
∴BD=CD,
∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°,
又∠1=∠2,
∴△BED≌△CFD(AAS),
∴BE=CF.
(本题还可以作AN⊥BC于N,利用等底等高的两个三角形的面积相等的性质证明)
点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,同时掌握全等三角形的性质.

练习册系列答案
相关题目