Question

已知x=1是二次方程（m²-1）x²-mx+m²=0的一个根，那么m的值是（ ）
A．或-1
B．或1
C．或1
D．

Answer 1

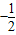
【答案】分析：将x=1代入已知方程列出关于m的新方程，通过解新方程可以求得m的值．注意：二次项系数不为零．
解答：解：∵（m²-1）x²-mx+m²=0是二次方程，
∴m²-1≠0，即m≠±1．
∵x=1是二次方程（m²-1）x²-mx+m²=0的一个根，
∴m²-1-m+m²=0，
解得，m=-，或m=1（不合题意，舍去）．
故选D．
点评：本题考查的是一元二次方程的根即方程的解的定义．一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值．即用这个数代替未知数所得式子仍然成立．