Question

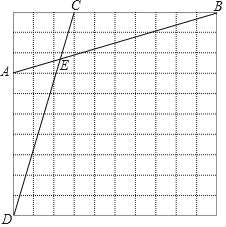
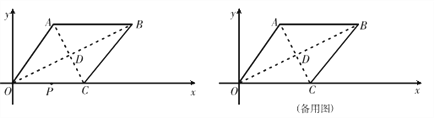
【题目】如图，在菱形 OA BC 中，已知点 B（8，4），C（5，0），

点 D 为 OB、AC 交点，点 P 从原点出发向 x 轴正方向运动；

（1） 在点 P 运动过程中，若∠OBP=900，求出点 P 坐标；

（2） 在点 P 运动过程中，若∠PDC+∠BCP=900，求出点 P 坐标；

（3） 点 P 在（2）的位置时停止运动，点 M 从点 P 出发沿 x 轴正方向运动，连结 BM，若点 P 关于BM 的对称点 P’到 AB 所在直线的距离为 2，求此时点 M 的坐标.

Answer 1

【答案】（1）（10,0）（2）(8，0)（3）点M的坐标为(8+,0)或(8+4,0)

【解析】分析：（1）根据菱形的性质有OD=BD，根据∠OBP=90 ，得到CD∥BP，根据中位线的性质求解即可.

根据 得到,求出,得到点P在以OB为直径的⊙D上，即可求解.

过点P′作P′N⊥AB交直线AB于点N，交轴于点K，记BM与PP′交点为L，分点P′在直线AB下方时和点P′在直线AB上方时两种情况进行讨论即可.

详解：（1）在菱形OABC中，有OD=BD，

∵∠OBP=90，∴CD∥BP

∵OD=BD，∴OC=PC

∵C（5,0），

∴P

(2)∵

∴,

∵OC=BC，∴,

∵

,

∴

∴,

∵D为OB中点,

∴点P在以OB为直径的⊙D上，

∴

故点P(8，0).

（3）过点P′作P′N⊥AB交直线AB于点N，交轴于点K，记BM与PP′交点为L

①如图，当点P′在直线AB下方时，

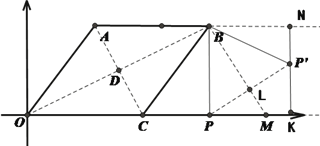
∵点P与点P′关于BM对称

∴

∵ ,

∴Rt△BNP′≌Rt△PKP′,

∴

即为等边三角形，

在Rt△PLM中，∵，∴PM2=22+（PM）2

解得PM=,∴OM=8+,

∴M1(8+,0),

②如图，当点P′在直线AB上方时

∵点P与点P′关于BM对称

∴

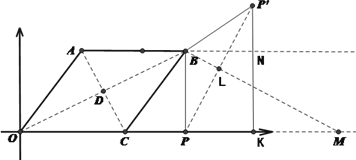
在中，

∵′,∴,

∴

∵

∵

∵

在Rt△BPM中,

∵BP=4,∴PM=BP=4

∴OM=8+4 ,

∴M2(8+4,0)

故点M的坐标为(8+,0)或(8+4,0)