题目内容
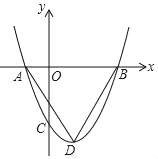
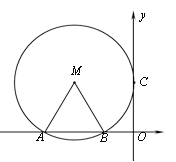
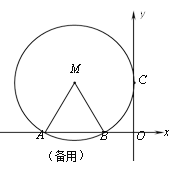
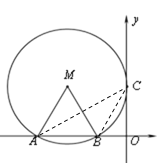
【题目】如图,在平面直角坐标系中,点M的坐标是(-2,![]() ),⊙M与y轴相切于点C,与x轴相交于A,B两点.
),⊙M与y轴相切于点C,与x轴相交于A,B两点.
(1)证明:△MAB是等边三角形.
(2)在⊙M上是否存在点D,使△ACD是直角三角形,若存在,试求点D的坐标;若不存在,请说明理由.
(3)若P(m,n)是过A,B,C三点的抛物线上一点,当∠APB≤30°时,直接写出m的取值范围.
【答案】(1)详见解析;(2)D点的坐标为(-4,![]() )或D(-1,
)或D(-1,![]() );(3)m≥0或m≤-4.
);(3)m≥0或m≤-4.
【解析】
(1)连MC,则OM⊥y轴于点C,过点M作MN⊥x轴于点N,根据点M的坐标得到MB、MN,再根据勾股定理求出BN即可求出AB的长度,由此得到结论;
(2)由△ACD是直角三角形分三种情况分别求出点D的坐标;
(3)连接AC、BC,根据等边三角形的性质及圆周角定理求出∠ABC的度数,确定过A,B,C三点的抛物线上点C的对称点的坐标即可得到答案.
(1)证明:连MC,则OM⊥y轴于点C,且MC=2,
过点M作MN⊥x轴于点N,
∵点M的坐标是(-2,![]() ),
),
∴MN=![]() ,
,
∵MA=MB=MC=2,
∴![]() ,
,
∴AB=2=MA=MB,
∴△MAB是等边三角形.

(2)分三种情况
第一种情况,
当以A为直角顶点时,CD为直径,
∴CD=4,
∴D(-4,![]() );
);
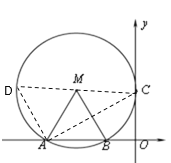
第二种情况,
当点C为直角顶点时,
AD为直径,
OB=2-1=1,
连接BD,则DB⊥x轴,
由勾股定理得:BD=![]() ,
,
∴D(-1,![]() );
);
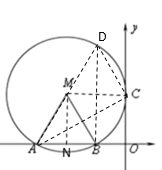
第三种情况,
当点D为直角顶点时,
AC不可能为直径,
故不可能D为直角顶点,
所以所求D点的坐标为(-4,![]() )或D(-1,
)或D(-1,![]() );
);
(3)连接AC、BC,
∵△MAB是等边三角形,
∴∠AMBA=60°,
∴∠ACB=30°,
∵过点A、B、C的抛物线的对称轴是直线x=-2,C(0,2),
∴点C的对称点的坐标是(-4,2),
∴当∠APB≤30°时,m≥0或m≤-4.

 阅读快车系列答案
阅读快车系列答案【题目】在一个不透明的口袋里装有若干个质地相同的红球,为了估计袋中红球的数量,某学习小组做了摸球试验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出1个球并记下颜色,再把它放回袋中,多次重复摸球.下表是多次摸球试验汇总后统计的数据:
摸球的次数 | 150 | 200 | 500 | 900 | 1 000 | 1 200 |
摸到白球的频数 | 51 | 64 | 156 | 275 | 303 | 361 |
摸到白球的频率 | 0.320 | 0.312 | 0.306 | 0.303 | 0.302 | 0.301 |
(1)请估计:当摸球的次数很大时,摸到白球的频率将会接近______;假如你去摸一次,你摸到红球的概率是______;(精确到0.1)
(2)试估计口袋中红球有多少个.