��Ŀ����
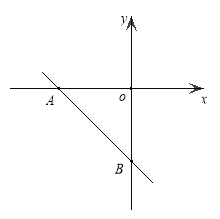
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���![]() �ֱ���x�ᡢy���ཻ��A��B���㣬���κ���
�ֱ���x�ᡢy���ཻ��A��B���㣬���κ���![]() ��ͼ����A��
��ͼ����A��
��1����֤�����κ���![]() ��ͼ����x�����������㣻
��ͼ����x�����������㣻
��2�������κ���![]() ͼ��Ķ���D��ֱ��AB�ϣ���m��n��ֵ��
ͼ��Ķ���D��ֱ��AB�ϣ���m��n��ֵ��
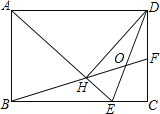
��3������κ���![]() ��ͼ����x�����һ������Ϊ��C������D����x��ĶԳƵ���Ϊ��E����AE��ACΪ�ڱ���ƽ���ı���EACF������F�ܷ��ڸö��κ�����ͼ���ϣ�����ڣ����������κ����ı���ʽ��������ڣ���˵�����ɣ�
��ͼ����x�����һ������Ϊ��C������D����x��ĶԳƵ���Ϊ��E����AE��ACΪ�ڱ���ƽ���ı���EACF������F�ܷ��ڸö��κ�����ͼ���ϣ�����ڣ����������κ����ı���ʽ��������ڣ���˵�����ɣ�
���𰸡���1��֤����������2��4��3��6��9��3��P��-1��![]() ��
��
��������
�����������1�����ݴ���ϵ������ö��κ����Ľ���ʽ��Ȼ����ݸ����б�ʽ��֤����
��2�����ݶ��κ����Ķ�����������m��n��ֵ��
��3������B����������m��ֵ�����ɵö��κ����Ľ���ʽ��Ȼ����E��ĺ�����Ϊt�����E������꣬�����ֱ��AE���ɴ����P�������.
�����������1��A����3��0����B��0����3����
���κ���![]() ��ͼ����C��-6��18-n������n=3m��9��
��ͼ����C��-6��18-n������n=3m��9��
��![]() .
.
��![]() =
=![]() =
=![]() ��
��
��![]() ��
��
��![]() ��
��
����κ���![]() ��ͼ����x�����������㣻
��ͼ����x�����������㣻
��2�������![]() ����
����![]()
����������![]() ��
��![]() ����
����
��Ϊ���κ���![]() ͼ��Ķ�����ֱ��AB�ϣ�
ͼ��Ķ�����ֱ��AB�ϣ�
����![]() ����ã�
����ã�![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��3��������![]() ����B��0��-3����
����B��0��-3����
��m=2
��ʱ������ϵʽΪ![]() ����֤��A����������.
����֤��A����������.
���E�ĺ�����Ϊt����-3+1����t +1��=![]()
��![]() �� ��õ�E������Ϊ��
�� ��õ�E������Ϊ��![]() ��
��![]() ����
����
��ֱ��AE��Ӧ�ĺ�����ϵʽ:![]() ��
��
��õ�P��-1��![]() ��.
��.

 ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�