题目内容
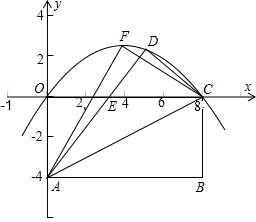 如图,四边形OABC是矩形,OA=4,OC=8,将矩形OABC沿直线AC折叠,使点B落在D处,AD交OC于E.
如图,四边形OABC是矩形,OA=4,OC=8,将矩形OABC沿直线AC折叠,使点B落在D处,AD交OC于E.(1)求OE的长;
(2)求过O,D,C三点抛物线的解析式;
(3)若F为过O,D,C三点抛物线的顶点,一动点P从点A出发,沿射线AB以每秒1个单位长度的速度匀速运动,当运动时间t(秒)为何值时,直线PF把△FAC分成面积之比为1:3的两部分.
分析:(1)已知四边形OABC是矩形,证明△CDE≌△AOE推出OE2+OA2=(AD-DE)2求出OE.
(2)本题要借助辅助线的帮助,证明△DGE≌△CDE.根据线段比求出DG,EG以及点D的坐标.列出解析式求出a,b的值.
(3)设直线AC的解析式为y=kx+b,把顶点坐标代入求出k,b.证明△AMH∽△AOC推出m的值.
(2)本题要借助辅助线的帮助,证明△DGE≌△CDE.根据线段比求出DG,EG以及点D的坐标.列出解析式求出a,b的值.
(3)设直线AC的解析式为y=kx+b,把顶点坐标代入求出k,b.证明△AMH∽△AOC推出m的值.
解答: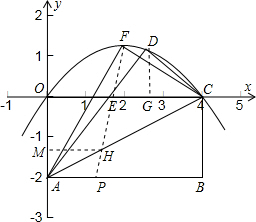 解:(1)∵四边形OABC是矩形,
解:(1)∵四边形OABC是矩形,
∴∠CDE=∠AOE=90°,OA=BC=CD.
又∵∠CED=∠OEA,
∴△CDE≌△AOE.
∴OE=DE.
∴OE2+OA2=(AD-DE)2,
即OE2+42=(8-OE)2,
解之,得OE=3.
(2)EC=8-3=5.如图,过D作DG⊥EC于G,
∴△DGE∽△CDE.
∴
=
,
=
.
∴DG=
,EG=
.
∴D(
,
).
因O点为坐标原点,
故可设过O,C,D三点抛物线的解析式为y=ax2+bx.
∴
解之,得
y=-
x2+
x
(3)∵抛物线的对称轴为x=4,
∴其顶点坐标为(4,
).
设直线AC的解析式为y=kx+b,
则
解之,得
∴y=
x-4.
设直线FP交直线AC于H(m,
m-4),过H作HM⊥OA于M.
∴△AMH∽△AOC.
∴HM:OC=AH:AC.
∵S△FAH:S△FHC=1:3或3:1,
∴AH:HC=1:3或3:1,
∴HM:OC=AH:AC=1:4或3:4.
∴HM=2或6,
即m=2或6.
∴H1(2,-3),H2(6,-1).
直线FH1的解析式为y=
x-
.
当y=-4时,x=
.
直线FH2的解析式为y=-
x+
.
当y=-4时,x=
.
∴当t=
秒或
秒时,
直线FP把△FAC分成面积之比为1:3的两部分.
 解:(1)∵四边形OABC是矩形,
解:(1)∵四边形OABC是矩形,∴∠CDE=∠AOE=90°,OA=BC=CD.
又∵∠CED=∠OEA,
∴△CDE≌△AOE.
∴OE=DE.
∴OE2+OA2=(AD-DE)2,
即OE2+42=(8-OE)2,
解之,得OE=3.
(2)EC=8-3=5.如图,过D作DG⊥EC于G,
∴△DGE∽△CDE.
∴
| DE |
| EC |
| DG |
| CD |
| DE |
| EC |
| EG |
| DE |
∴DG=
| 12 |
| 5 |
| 9 |
| 5 |
∴D(
| 24 |
| 5 |
| 12 |
| 5 |
因O点为坐标原点,
故可设过O,C,D三点抛物线的解析式为y=ax2+bx.
∴
|
解之,得
|
| 5 |
| 32 |
| 5 |
| 4 |
(3)∵抛物线的对称轴为x=4,
∴其顶点坐标为(4,
| 5 |
| 2 |
设直线AC的解析式为y=kx+b,
则
|
|
∴y=
| 1 |
| 2 |
设直线FP交直线AC于H(m,
| 1 |
| 2 |
∴△AMH∽△AOC.
∴HM:OC=AH:AC.
∵S△FAH:S△FHC=1:3或3:1,
∴AH:HC=1:3或3:1,
∴HM:OC=AH:AC=1:4或3:4.
∴HM=2或6,
即m=2或6.
∴H1(2,-3),H2(6,-1).
直线FH1的解析式为y=
| 11 |
| 4 |
| 17 |
| 2 |
当y=-4时,x=
| 18 |
| 11 |
直线FH2的解析式为y=-
| 7 |
| 4 |
| 19 |
| 2 |
当y=-4时,x=
| 54 |
| 7 |
∴当t=
| 18 |
| 11 |
| 54 |
| 7 |
直线FP把△FAC分成面积之比为1:3的两部分.
点评:本题考查的是相似三角形的判定以及二次函数的综合运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ.
动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ.  在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.
在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.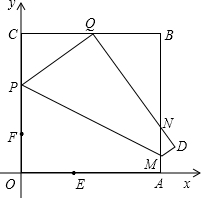
 (2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数
(2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数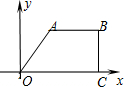 是( )
是( )