题目内容
【题目】概念学习
规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．
从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．
理解概念
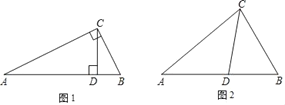
（1）如图1，在Rt△ABC中，∠ACB＝90°，CD⊥AB，请写出图中两对“等角三角形”．
概念应用
（2）如图2，在△ABC中，CD为角平分线，∠A＝40°，∠B＝60°．求证：CD为△ABC的等角分割线．
（3）在△ABC中，∠A＝42°，CD是△ABC的等角分割线，直接写出∠ACB的度数．
【答案】（1）△ABC与△ACD，△ABC与△BCD，△ACD与△BCD是“等角三角形”；（2）见解析；（3）∠ACB的度数为111°或84°或106°或92°
【解析】
（1）根据题中给出的“等角三角形”的定义即可解答；
（2）通过三角形内角和定理求出∠ACB为80°，然后再由角平分线的定义可得到∠ACD=∠DCB=
∠ACB=40°，最后通过 “等角分割线”的定义进行证明；
（3）需分情况讨论，当△ACD是等腰三角形时DA=DC或DA=AC，当△BCD是等腰三角形时DB=BC或DC=BD，然后根据等腰三角形的性质和三角形的内角和定理进行求解．
解：（1）△ABC与△ACD，△ABC与△BCD，△ACD与△BCD是“等角三角形”；
（2）∵在△ABC中，∠A＝40°，∠B＝60°
∴∠ACB＝180°﹣∠A﹣∠B＝80°
∵CD为角平分线，
∴∠ACD＝∠DCB＝∠ACB＝40°，
∴∠ACD＝∠A，∠DCB＝∠A，
∴CD＝DA，
∵在△DBC中，∠DCB＝40°，∠B＝60°，
∴∠BDC＝180°﹣∠DCB﹣∠B＝80°，
∴∠BDC＝∠ACB，
∵CD＝DA，∠BDC＝∠ACB，∠DCB＝∠A，
∠B＝∠B，
∴CD为△ABC的等角分割线；
（3）当△ACD是等腰三角形，DA＝DC时，∠ACD＝∠A＝42°，
∴∠ACB＝∠BDC＝42°+42°＝84°，
当△ACD是等腰三角形，DA＝AC时，∠ACD＝∠ADC＝69°，
∠BCD＝∠A＝42°，
∴∠ACB＝69°+42°＝111°，
当△BCD是等腰三角形，DC＝BD时，∠ACD＝∠BCD＝∠B＝46°，
∴∠ACB＝92°，
当△BCD是等腰三角形，DB＝BC时，∠BDC＝∠BCD，
设∠BDC＝∠BCD＝x，
则∠B＝180°﹣2x，
则∠ACD＝∠B＝180°﹣2x，
由题意得，180°﹣2x+42°＝x，
解得，x＝74°，
∴∠ACD＝180°﹣2x＝32°，
∴∠ACB＝106°，
∴∠ACB的度数为111°或84°或106°或92°．
