题目内容
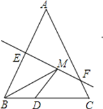
【题目】如图,已知Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线分别交BC,CD于E、F.
(1)试说明△CEF是等腰三角形.
(2)若点E恰好在线段AB的垂直平分线上,试说明线段AC与线段AB之间的数量关系.

【答案】(1)见解析(2)见解析
【解析】
(1)首先根据条件∠ACB=90°,CD是AB边上的高,可证出∠B+∠BAC=90°,∠CAD+∠ACD=90°,再根据同角的补角相等可得到∠ACD=∠B,再利用三角形的外角与内角的关系可得到∠CFE=∠CEF,最后利用等角对等边即可得出答案;
(2)线段垂直平分线的性质得到AE=BE,根据等腰三角形的性质得到∠EAB=∠B,由于AE是∠BAC的平分线,得到∠CAE=∠EAB,根据直角三角形的性质即可得到结论.
解:(1)∵∠ACB=90°,
∴∠B+∠BAC=90°,
∵CD⊥AB,
∴∠CAD+∠ACD=90°,
∴∠ACD=∠B,
∵AE是∠BAC的平分线,
∴∠CAE=∠EAB,
∵∠EAB+∠B=∠CEA,∠CAE+∠ACD=∠CFE,
∴∠CFE=∠CEF,
∴CF=CE,
∴△CEF是等腰三角形;
(2)∵点E恰好在线段AB的垂直平分线上,
∴AE=BE,
∴∠EAB=∠B,
∵AE是∠BAC的平分线,
∴∠CAE=∠EAB,
∴∠CAB=2∠B,
∵∠ACB=90°,
∴∠CAB+∠B=90°,
∴∠B=30°,
∴AC=![]() AB.
AB.

 名校课堂系列答案
名校课堂系列答案【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.