题目内容
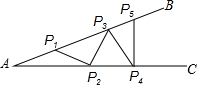
 如图钢架BAC中,焊上等长的钢条来加固钢架,若P1A=P1P2,量得∠A=15°,则这样的钢管最多可以焊
如图钢架BAC中,焊上等长的钢条来加固钢架,若P1A=P1P2,量得∠A=15°,则这样的钢管最多可以焊5
5
条.分析:由于焊上的钢条长度相等,并且A P1=P1P2,所以∠A=∠P1P2A,则可算出∠P2P1P3的度数,并且和∠P1P3P2度数相等,根据平角的度数为180度和三角形内角和为180度,结合等腰三角形底角度数小于90度即可求出最多能焊上的钢条数.
解答: 解:如图:
解:如图:
∵∠A=∠P1P2A=15°,
∴∠P2P1P3=30°,∠P1P3P2=30°,
∴∠P1P2P3=120°,
∴∠P3P2P4=45°,
∴∠P3P4P2=45°,
∴∠P2P3P4=90°,
∴∠P4P3P5=60°,
∴∠P3P5P4=60°,
∴∠P3P4P5=60°,
∴∠P5P4P6=75°,
∴∠P4P6P5=75°,
∴∠P4P5P6=30°,
∴∠P6P5P7=90°.
此时就不能再往上焊接了,
综上所述总共可焊上5条.
故答案为:5.
 解:如图:
解:如图:∵∠A=∠P1P2A=15°,
∴∠P2P1P3=30°,∠P1P3P2=30°,
∴∠P1P2P3=120°,
∴∠P3P2P4=45°,
∴∠P3P4P2=45°,
∴∠P2P3P4=90°,
∴∠P4P3P5=60°,
∴∠P3P5P4=60°,
∴∠P3P4P5=60°,
∴∠P5P4P6=75°,
∴∠P4P6P5=75°,
∴∠P4P5P6=30°,
∴∠P6P5P7=90°.
此时就不能再往上焊接了,
综上所述总共可焊上5条.
故答案为:5.
点评:本题主要考点:等腰三角形两底角相等,三角形内角和为180度,平角度数为180度等.结合图形依次算出各角的度数,根据等腰三角形底角小于90度判断何时不能再焊接上.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目

 如图钢架BAC中,焊上等长的钢条p1p2,p2p3,p3p4,p4p5来加固钢架,若P1A=P1P2,则∠A的取值范围
如图钢架BAC中,焊上等长的钢条p1p2,p2p3,p3p4,p4p5来加固钢架,若P1A=P1P2,则∠A的取值范围